Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 5

;  x = r cos a ;  y = r sin a ,

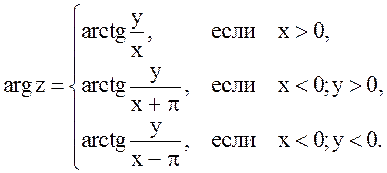                                    (1.46)

Запись комплексного числа в виде

z = r(cos a + i sin a)

называется его тригонометрической формой. С помощью равенства Эйлера

exp(ia) = cos a + i sin a

можно записать комплексное число в показательной форме

z = r exp(ia)                                                            (1.47)

В зависимости от действий над комплексными числами применяются различные виды их представления.

При сложении и вычитании применяется алгебраическая форма представления комплексных чисел

z₃ = z₁ + z₂ = x₁ + i y₁ + x₂ + i y₂ = x₁ + x₂ + i (y₁ + y₂),

z₃ = z₁ - z₂= x₁ + i y₁ - x₂ - i y₂ = x₁ - x₂ + i (y₁ - y₂)                             (1.48)

При умножении и делении предпочтительно применение показательной формы представления комплексных чисел

                     (1.49)

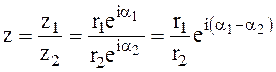                                            (1.50)

При возведении комплексного числа в натуральную степень и извлечении корня натуральной степени применяются показательная и тригонометрическая формы представления комплексных чисел

,                                                             (1.51)

,                                                  (1.52)

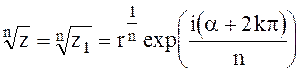,                                                 (1.53)

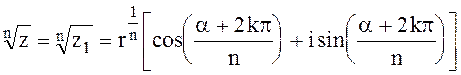                                 (1.54)

где k = 0, 1, 2, 3, ..., n - 1.

Возможны два вида комплексных функций: комплексные функции действительного переменного, комплексные функции комплексного переменного. Рассмотрим плоскость комплексного переменного

z = x + iy

и предположим, что действительная и мнимая части z являются непрерывными функциями x(t) и y(t) некоторого действительного переменного t, заданными на промежутке a < t < b. Будем по определению считать, что тем самым задана функциональная зависимость

z = z(t)

между независимым действительным переменным t и комплексным переменным z.

При изменении переменного t в пределах от a до b точка М(х, у), изображающая комплексное число z, опишет на плоскости линию, называемую годографом функции z = z(t).

Предположим, что функции x(t) и y(t) не только непрерывны, но и дифференцируемы на [a,b]. Будем называть производной функции z = z(t) выражение

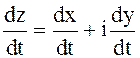                                                         (1.55)

Принимая во внимание то, что z(t) геометрически изображается некоторой кривой, называемой годографом, можно сказать, что если эта функция дифференцируема, причем  ¹ 0, то ее годограф в каждой точке имеет касательную.

Комплексные функции действительного переменного, о  которых шла речь выше, наиболее часто применяются при рассмотрении гармонических процессов. При этом используется формула Эйлера

                     (1.56)

Действительная часть z

Re z = r cos(wt + y)

описывает гармоническое колебание, с частотой w, амплитудой А и фазой y.

Комплексная форма записи колебаний очень удобна при решении многих задач в электротехнике и радиотехнике. В этом случае напряжения и токи записываются в виде комплексных величин и вводится понятие полного сопротивления (импеданса), включающего активную и реактивную составляющие.

                                                    (1.57)

                                                         (1.58)

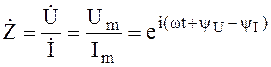                                   (1.59)

Здесь U_m, I_m - амплитуды напряжения и тока, y_U, y_I - фазы напряжения и тока,  - комплексное сопротивление.

ГЛАВА 2. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ

2.1. Система уравнений электромагнитного поля

Электромагнитное поле представляет собой одну из форм существования материи и описывается с помощью  четырех векторных величин: вектора напряженности электрического поля Е [В/м], вектора магнитной индукции В [Вб/м²], вектора напряженности магнитного поля Н [А/м], вектора электрического смещения (электрической индукции) D [Кл/м²]. Все векторные величины являются функциями координат и времени. Векторы В и Е оказывают механическое воздействие на заряженные частицы, помещаемые в электромагнитное поле.

F = F_э+ F_м= qE + q[V, B],                                                (2.1)