Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 29

и 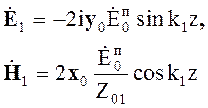                                                                                  (5.64)

Выражения (5.63) и (5.64) не содержат волнового множителя, то есть поле описываемое ими не имеет волнового характера. Комплексный вектор Пойтинга

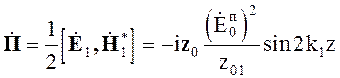                                           (5.65)

имеет только мнимую составляющую, которая характеризует реактивную (запасенную) энергию. Среднее значение вектора Пойтинга

говорит о том, что энергия не переносится.

Так как электромагнитное поле, описываемое выражениями (5.63) и (5.64), образуется в результате интерференции падающей и отраженной волной и энергию не переносит, то его принято называть стоячей волной.

Основные признаки стоячей волны. Векторы электромагнитного поля  и  имеют фазовый сдвиг, равный p/2. Амплитуды составляющих поля Е и Н

                       и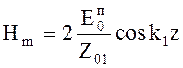  

изменяются по гармоническому закону вдоль оси z, причем H_m имеет максимальное значение на поверхности проводника, а E_m минимальное значение, равное нулю. Энергия вдоль оси z не переносится. Фазовая скорость стоячей волны , следовательно, векторы поля в точках, расположенных на оси z имеют одинаковую фазу колебаний. Векторы поля в плоскостях, перпендикулярных оси z, имеют одинаковую амплитуду. Скорость переноса энергии V_э = 0, то есть энергия вдоль оси z не переносится.

Домножая, комплексные амплитуды полей (5.64) на  и выделяя действительную часть, получим выражения для описания поля стоячей волны

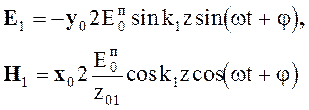                                                 (5.66)

На рис. 5.5. показан характер изменения амплитуд векторов поля E_m и H_m в зависимости от расстояния до идеально проводящей поверхности.

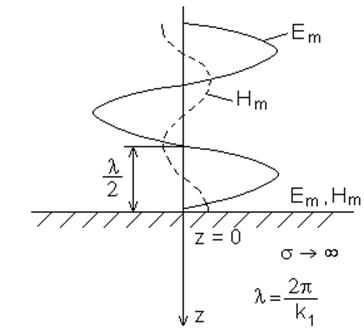
Рис. 5.5. Изменения амплитуд векторов Е и Н в стоячей волне.

5.7. Приближенные граничные условия Леонтовича-Щукина

В реальных задачах происходит взаимодействие электромагнитного поля с металлическими телами, имеющими конечное значение электрической проводимости. Решение таких задач можно значительно упростить введением приближенных граничных условий Леонтовича-Щукина. В отличие от обычных граничных условий, связывающих значения составляющих поля на границе раздела в разных средах, граничные условия Леонтовича-Щукина выражают связь между составляющими векторов  и  в одной среде.

Угол преломления при прохождении волны в поглощающую среду описывается выражением

При больших значениях проводимости

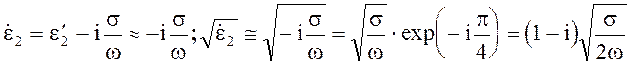
Поэтому

и при больших значениях s   .

При любом угле падения можно для металлов считать, что угол преломления равен нулю и волна прошедшая в металл (среда 2) распространяется по нормали к поверхности раздела.

Так как предполагается, что волна во второй среде распространяется вдоль нормали к поверхности раздела, то векторы  и  должны быть параллельны поверхности раздела. На границе раздела должны выполняться граничные условия для тангенциальных составляющих векторов  и .

   и                                           (5.67)

Так как во второй среде других составляющих поля, кроме тангенциальных, нет, то можно записать

или в векторной форме

                                                    (5.68)

Из (5.67) и (5.68) можно записать

                                          (5.69)

Последнее соотношение называется приближенным условием Леонтовича-Щукина. Из него можно сделать вывод, что на поверхности реального проводника касательная составляющая напряженности электрического поля отлична от нуля. В инженерных расчетах касательную составляющую вектора  на поверхности реального проводника обычно не учитывают, кроме тех случаев, когда требуется определить потери в проводнике.

ЧАСТЬ 2

НАПРАВЛЕННЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

И НАПРАВЛЯЮЩИЕ СИСТЕМЫ

ГЛАВА 6

НАПРАВЛЕННЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В РАЗЛИЧНОГО ВИДА СТРУКТУРАХ

6.1. Электромагнитные волны в продольно-однородных структурах

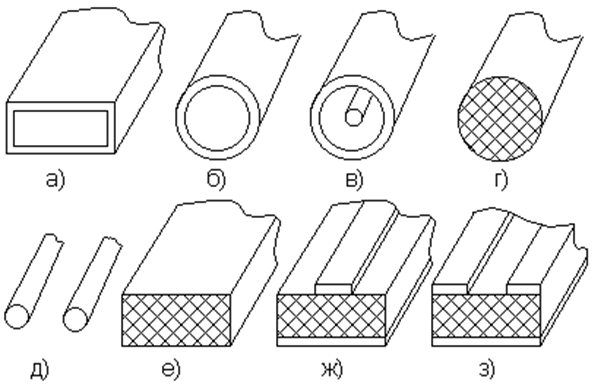
Продольно-однородная структура - такая пространственная структура, в которой все ее сечения плоскостями z = const, где z - продольная координата, тождественны. Примеры таких структур приводятся на рис. 6.1.