Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 15

Внешняя задача электродинамики имеет единственное решение, если на границе S объема V выполняются те же условия, что и для внутренней задачи, а на границе S₁ (рис.3.2.), удаленной на бесконечность, выполняются условия излучения

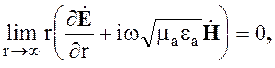
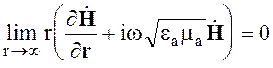.                                                                  (3.7)

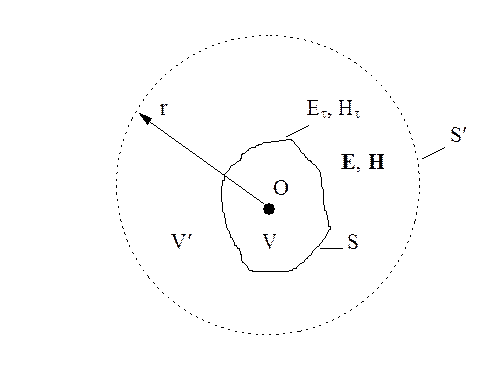
Рис. 3.2. Внешняя задача электродинамики.

В случае внешней задачи рассматривают единственность решения для поля в объеме V', ограниченном поверхностью S и S'.

Доказательство. Проведем из произвольной точки объема V сферу радиусом r и будем иметь поверхность S' в виде сферы. Уравнение баланса для средних значений мощности в объеме V' в случае рассмотрения разностного решения принимает вид

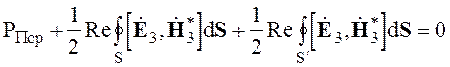                                      (3.8)

Перейдем к пределу при . Если окажется, что третий член выражения (3.8) в результате такого перехода обратится в нуль, то доказательство теоремы далее аналогично доказательству для внутренней задачи. Условие

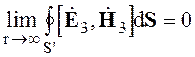                                                                       (3.9)

очевидно выполняется при убывании амплитуд векторов  и  более быстро, чем 1 / r, так как поверхность сферы S' возрастает пропорционально r².

Более строго условия излучения записываются в виде (3.7), который говорит о том, что амплитуды векторов  могут убывать и как 1 / r.

3.3. Принцип суперпозиции

Для линейной изотропной среды дифференциальные уравнения Максвелла будут линейными. Линейная комбинация решений таких уравнений также является решением уравнений. Из этого положения непосредственно вытекает принцип суперпозиции, который заключается в следующем. Пусть в рассматриваемом объеме распределено n систем источников электромагнитного поля  которые не оказывают никакого влияния друг на друга. При отсутствии всех остальных систем источников первая система  создает поле . Вторая система источников  при отсутствии всех остальных создает поле  и так далее.

В соответствии с принципом суперпозиции все n систем источников при прежнем их расположении будут создавать общее поле, напряженность которого определяется векторной суммой полей отдельных источников

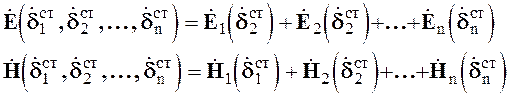(3.10)

Принцип суперпозиции неприменим к определению энергии суммарного поля

Принцип перестановочной двойственности

Принцип перестановочной двойственности значительно сокращает расчеты при решении многих задач в теории антенн. Принцип вытекает из симметрии уравнений Максвелла.

Предположим, что наряду с электрическими источниками  существуют магнитные источники . Физический смысл подобного предположения поясняется в теории антенн.

Система уравнений Максвелла для случая возбуждения поля электрическими источниками имеет вид

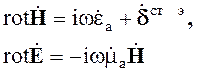                                                                       (3.11)

Вторую систему уравнений запишем для случая возбуждения электромагнитного поля магнитными источниками

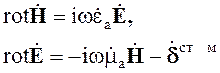                                                                 (3.12)

С физической точки зрения системы уравнений (3.11) и (3.12) описывают разные объекты. Первая описывает излучение проводника с током, а вторая - рамки с током. С математической точки зрения обе системы одинаковы. Если произвести замену по схеме

                                                      (3.13)

то одна система переходит в другую. Это свойство уравнений и выражает принцип перестановочной двойственности, который можно сформулировать следующим образом.

Если при решении задачи, описываемой одной из систем (3.11) или (3.12) найдены выражения для векторов поля  и при этом постоянные интегрирования определены из граничных условий для одного из векторов, то из указанных выражений можно получить выражения, являющееся решением другой задачи путем перестановки в них по схеме (3.13) при условии сохранения прежних граничных условий для другого вектора.

Наиболее удобно применять этот принцип для решения внешней задачи электродинамики, которая и является основной в теории антенн, так как граничные условия для векторов  (условия излучения) идентичны.