Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 27

Поле в среде 1 записывается в виде суммы падающей и отраженной волн

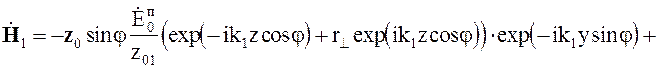                    (5.27)

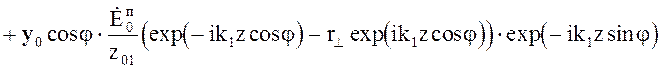
Поле во второй среде представляет собой прошедшую волну

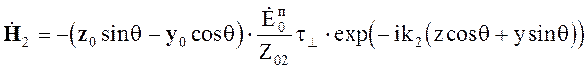                      (5.28)

5.2. Законы отражения и преломления для случая параллельной поляризации падающей волны

В этом случае вектор  лежит в плоскости падения, вектор  перпендикулярен плоскости падения, как показано на рис. 5.3. Все законы, кроме формул Френеля, аналогичны случаю перпендикулярной поляризации вектора  падающей волны. Для того чтобы получить формулы Френеля для случая параллельной поляризации, используем снова граничные условия для тангенциальных составляющих векторов  и  при z = 0.

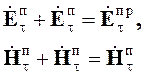
или в соответствии с рис. 5.3.,

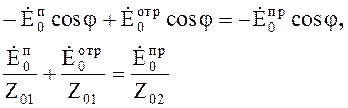                                (5.29)

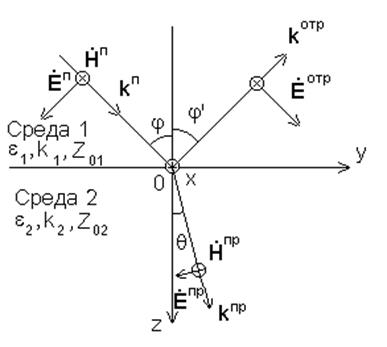
Рис. 5.3. Ориентация векторов поля при параллельной поляризации

падающей волны.

Разделив уравнение (5.29) на , получим

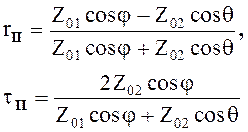                                                 (5.30)

Если вторая среда имеет потери, а первая среда воздух, тогда

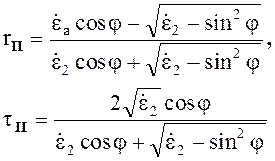                                            (5.31)

Поле в среде 1 описывается выражением

            (5.32)

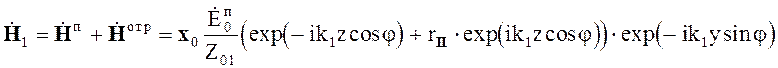
Поле в среде 2 представляет собой прошедшую волну

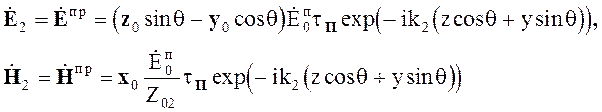                    (5.33)

В случае нормального падения j = 0, q = 0. Коэффициенты Френеля принимают вид

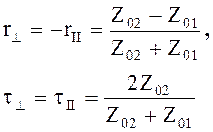                                                       (5.34)

5.3. Угол Брюстера и связанные с ним явления

Получим условия полного прохождения падающей волны во вторую среду. В этом случае коэффициент отражения равен нулю

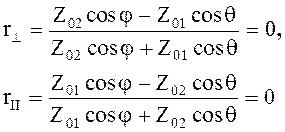                                           (5.35)

В случае перпендикулярной поляризации

или 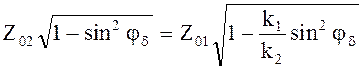   ,                                                 (5.36)

отсюда

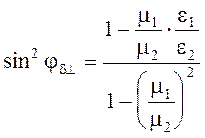                                              (5.37)

Видно, что для диэлектриков (m₁ = m₂ = 1) существование угла Брюстера невозможно. При m₁ ¹ m₂ и e₁ ¹ e₂ угол Брюстера существует, если выполняется условие

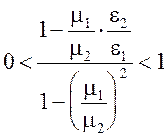                                                    (5.38)

В случае параллельной поляризации

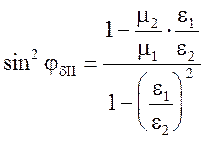                                              (5.39)

При m₁ = m₂, когда обе среды диэлектрики

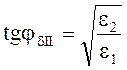.                                                          (5.40)

Существование угла Брюстера при параллельной поляризации падающей волны и m₁ ¹ m₂ , возможно при выполнении условия

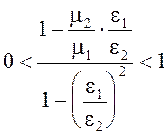                                                    (5.41)

Интересное следствие. Падая на границу раздела двух диэлектриков под углом Брюстера j_БII волна с эллиптической поляризацией вектора Е создает отраженную волну с линейной поляризацией вектора Е, причем в этой волне вектор Е перпендикулярен плоскости падения.

5.4. Поверхностные волны

При падении плоской однородной волны из среды более плотной в среду менее плотную угол преломления всегда больше угла падения. При определенном угле падения, назовем его критическим и обозначим j_кр, угол преломления окажется равным p/2 и будет выполняться соотношение

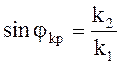                                                            (5.42)

так как  .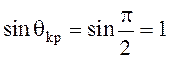

Представляет большой интерес рассмотрение явлений, происходящих при падении волны на поверхность раздела под углом j > j_кр, когда синус угла преломления становится больше единицы

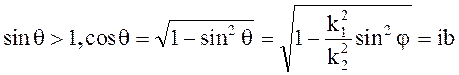                        (5.43)

В этом случае косинус угла преломления становится чисто мнимой величиной. С учетом (5.43) выражение для коэффициентов отражения r_^ и r_II принимают вид

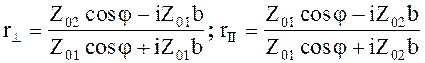                             (5.44)

Модули коэффициентов ½r_^½ = ½r_II½ = 1, а фазы коэффициентов зависят от угла падения и различны для волн с перпендикулярной и параллельной поляризацией вектора Е

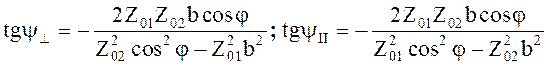                   (5.45)

Выражения для коэффициентов отражения принимают вид

                                                 (5.46)

Из выражений (5.24) и (5.30) получаем

 ;

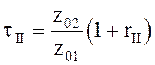
или 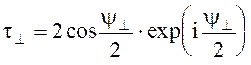   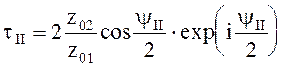;                    (5.47)

Выражения для поля в первой среде принимают вид в случае перпендикулярной поляризации

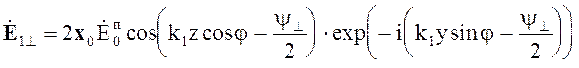
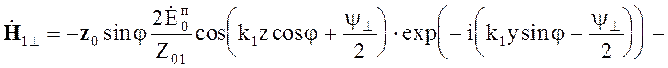          (5.48)

.

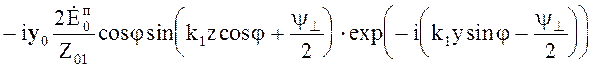В случае параллельной поляризации

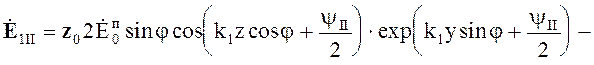
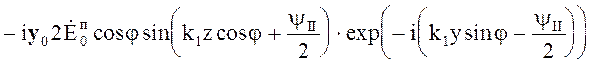;                    (5.49)

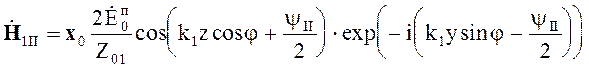
Выражения (5.48), (5.49) показывают, что поле в первой среде и в случае перпендикулярной, и в случае параллельной поляризации представляет собой плоскую волну, распространяющуюся вдоль оси у с фазовой скоростью