Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 25

Законы отражения и преломления рассматриваются для плоской границы раздела, используя при этом прямоугольную систему координат. Обычно систему координат располагают таким образом, чтобы координаты х и у лежали в плоскости раздела, а координата z была перпендикулярной ей.

В общем случае направление распространения волны, падающей на границу раздела () не совпадают ни с одной из координатных осей. Для указания направления движения волны введем координату z¢, совпадающую с направлением движения падающей волны, как показано на рис. 5.1.

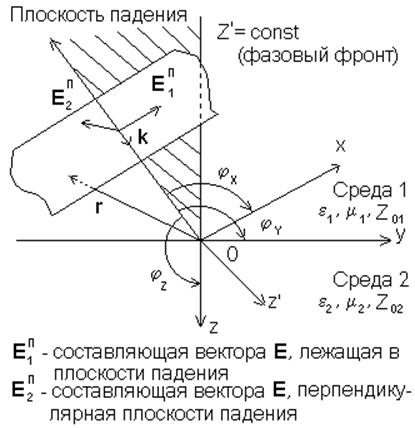
Рис.5.1. Падающая волна в декартовой системе координат

Волну с произвольной поляризацией всегда можно представить в виде двух волн, векторы поля которых взаимно перпендикулярны друг другу и имеют сдвиг по фазе f = y - j. Поэтому достаточно рассматривать два отдельных случая падения линейно поляризованных волн, которые отличаются ориентацией векторов на 90⁰ в пространстве.

На рис.5.1. показана плоскость, образованная направлением движения падающей волны и нормалью к поверхности раздела n₀. Эта плоскость называется плоскостью падения. При рассмотрении волны произвольной поляризации и ее представлении в виде двух волн с линейной поляризацией Е₁ и Е₂ и f = y - j ориентация векторов Е₁ и Е₂ выбирается так, чтобы один  из них был перпендикулярен плоскости падения, а другой лежал бы в плоскости падения.

Отдельно рассматриваются законы отражения и преломления для волны с перпендикулярной поляризацией (вектор Е₁ перпендикулярен плоскости падения) и законы отражения и преломления для волны с параллельной поляризацией (вектор Е лежит в плоскости падения). Затем складываются отраженные и преломленные волны с учетом их амплитуд и фазовых соотношений.

Направление движения волны удобно указывать, вводя понятие волнового вектора k, по величине равного волновому числу, а по направлению - указывающему направление движения волны.

Падающую волну легко записать в виде

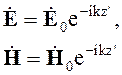                                                  (5.1)

Семейство плоскостей z¢ = const представляет собой плоскости равных фаз, перпендикулярные оси z¢. В векторном виде множитель kz¢ можно записать как

kz¢ = kr                                                          (5.2)

где  k - волновой вектор, r- радиус вектор.

Здесь

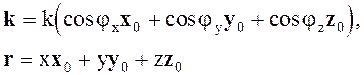
Следовательно,

kz¢ = kr = k(x cosj_x + y cos j_y + z cosj_z)

Выражения (5.1) принимают вид

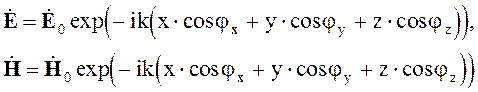                    (5.3)

Можно сделать вывод о том, что волновой множитель волны, распространяющейся под произвольным углом к плоскости раздела, в системе координат xyz, связанной с этой плоскостью, записывается в виде

                                (5.4)

5.1. Законы отражения  и преломления при падении электромагнитной волны на плоскую границу раздела. Перпендикулярная поляризация падающей волны

При указанной на рис.5.2. системе координат плоскость падения совпадает с плоскостью z0y, волна падает под углом j, направление падения волны  показывает вектор k^п. Параметры среды 1: e₁, k₁, Z₀₁. Параметры среды 2: e₂, k₂, Z₀₂. Угол j¢ - угол отражения. Угол q - угол преломления.

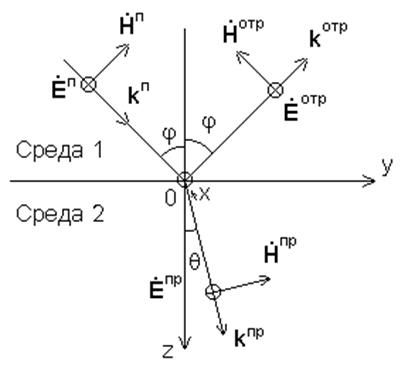
Рис. 5.2. Ориентация векторов поля при перпендикулярной поляризации падающей волны.

При падении волны на поверхность раздела происходит возбуждение вещества на поверхности раздела и в силу принципа причинности возможно возникновение волн, распространяющихся от поверхности как в среду 1, так и в среду 2. Волна, возбуждаемая в среде 1 называется отраженной, возбуждаемая в среде 2 - прошедшей. Величины относящиеся к падающей волне обозначаются индексом “п”, к отраженной - “отр”, к прошедшей - “пр”.

Выражения для падающей, отраженной и прошедшей волн принимают вид

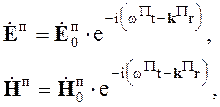
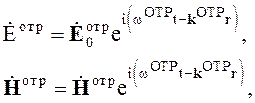                                                (5.5)

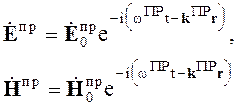
Законы отражения и преломления электромагнитных волн устанавливают соотношения между: w^п, w^отр, w^пр - частотами падающей, отраженной и прошедшей волн; k^пr, k^отрr, k^прr - направлениями волновых векторов падающей, отраженной и прошедшей волн и зависимостью этих направлений от параметров первой и второй среды;   - значениями комплексных векторных амплитуд векторов поля падающей, отраженной и прошедшей волн, то есть между взаимной ориентацией векторов, величинами их амплитуд и разностью фаз в зависимости от параметров первой и второй среды.