Траектория вектора частично поляризованной волны представляет собой эллипс, форма и размеры которого непрерывно изменяются во времени. При этом скорость изменения параметров эллипса на много меньше той скорости, с которой конец вектора описывает каждый эллипс. Примером частично поляризованной волны может служить сигнал, спектр которого содержит несколько гармоник.
Неполяризованная волна имеет такие флуктуации эллипса, при которых среднее за время наблюдения значение квадрата напряженности поля имеет одну и ту же величину для любого направления в плоскости, перпендикулярной направлению движения волны. Примером неполяризованной волны является солнечный свет.
Наибольшее практическое значение имеют полностью поляризованные волны. Далее будем рассматривать именно такие волны. Различают несколько видов поляризации полностью поляризованных волн: эллиптическую, круговую и плоскостную (линейную).
В зависимости от направления движения вектора различают правую и левую поляризацию волны. Правая поляризация такая, при которой если смотреть по направлению движения волны, конец вектора движется по часовой стрелке. Поляризация называется круговой, если конец одного из векторов поля описывает кривую в виде окружности. Поляризация называется плоскостной или линейной, если векторы поля ориентированы во времени всего периода колебаний в плоскости, которая называется плоскостью поляризации. Плоскость поляризации это плоскость, образованная направлением движения волны и вектором Е или Н.
Траектории векторов Е и Н для плоских однородных волн лежат в плоскости, перпендикулярной направлению распространения волн.
Решение волнового уравнения для случая плоских однородных волн было получено в виде
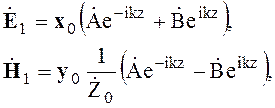
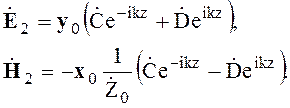
Суммарное поле прямых волн (волн, распространяющихся в положительном направлении оси Z)
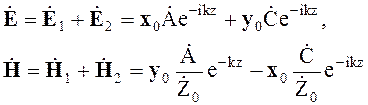(4.84)
В
дальнейшем будем рассматривать только векторы Е, так как в плоской
однородной волне векторы Е и Н взаимно перпендикулярны и связаны
соотношением E = [H, z0]
.
Поэтому форма траектории конца вектора Е совпадает с формой траектории
конца вектора Н. Изменяется только масштаб на множитель Z0.
Умножая первое уравнение (4.84) на 
и выделяя действительную
часть, получаем
(4.85)
Запишем в параметрическом виде выражение для траектории конца вектора Е в фиксированной точке пространства z = z1, например z = 0.
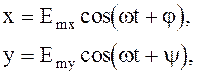(4.86)
Исключим из выражений временной множитель
.
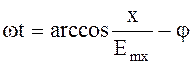Подставим во второе выражение (4.86) и получим после преобразований
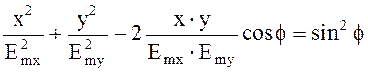, (4.87)
где f = j - y.
Выражение (4.87) описывает эллипс, большая ось которого (при отсчете от положительного направления оси х против часовой стрелки) составляет с осью x угол b, определяемый соотношением
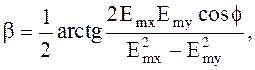0 £
b £
p (4.88)
Количественная оценка поляризации волны осуществляется с помощью параметров эллипса, который называется эллипсом поляризации и показан на рис. 4.4.
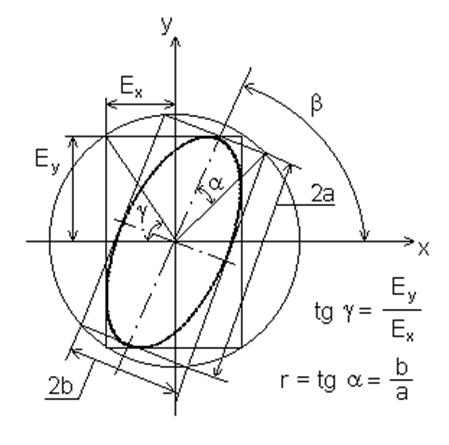
Рис. 4.4. Эллипс поляризации
Угол a называется углом эллиптичности.
r = tg a (4.89)
называется коэффициентом эллиптичности.
Построение эллипса поляризации производится по измеренным значениям Emx, Emy, f = y - j. Из выражения (4.88) определяется b, затем
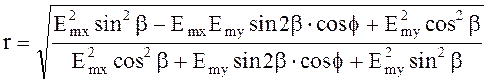(4.90)
Угол эллиптичности
a = arctg r
Большая полуось эллипса
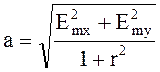(4.91)
Малая полуось эллипса
b = a½tg a½ = a½r½ (4.92)
Значения амплитуд Emx, Emy составляющих поля и разности фаз между ними полностью определяют вид поляризации.
Круговая поляризация. Векторы Е1 и Е2 взаимно перпендикулярны, амплитуды их равны Emx = Emy, а разность фаз f = p / 2. При этих условиях выражение (4.87) описывает окружность
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.