Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 16

При различных граничных условиях в первой и второй задачах принцип используется для получения общего интеграла для векторного поля, для которого заданы граничные условия во второй задаче, по общему интегралу для другого вектора, найденному в первой задаче. После этого определяются постоянные интегрирования из граничных условий для второй задачи.

3.4. Лемма Лоренца. Теорема взаимности

Лемма Лоренца устанавливает взаимосвязь между воздействующими друг на друга источниками и возбуждаемыми ими полями. Частным случаем леммы Лоренца является теорема взаимности.

Для вывода леммы Лоренца рассмотрим объем V, ограниченный поверхностью S, в котором расположены две системы источников  рис.3.3., заключенные в объемы V₁ и V₂. Первая система источников создает в каждой точке объема V поле , вторая система - поле .

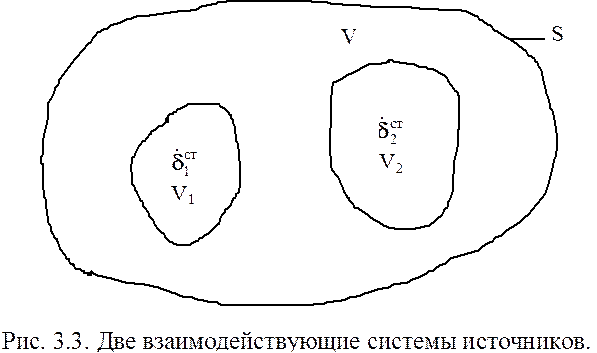
Согласно принципу суперпозиции дифференциальные уравнения для указанных полей можно записать как независимые, а затем рассмотреть влияние поля первой системы источников на вторую, а поля второй системы источников на первую.

Система 1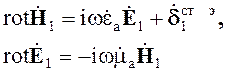  

Система 2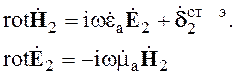  

Умножим скалярно первое уравнение системы 1 на , второе - на ; первое уравнение системы 2 - на , второе - на . После умножения вычтем из первого уравнения системы 1 второе уравнение системы 2, а из первого уравнения системы 2 - второе уравнение системы 1. В результате получим

                                  (3.14)

                                   (3.15)

Вычтем из уравнения (3.14) уравнение (3.15) и получим

                                         (3.16)

Выражение (3.16) называется леммой Лоренца в дифференциальной форме.

Интегрируя по объему V и применяя теорему Остроградского-Гаусса к левой части полученного выражения, имеем

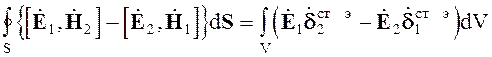                           (3.17)

Выражение (3.17) представляет собой лемму Лоренца в интегральном виде.

В случае рассмотрения внешней задачи электродинамики левый интеграл в выражении (3.17) при r ® ¥  обращается в нуль, если выполняются условия излучения (амплитуды убывают быстрее, чем 1 / r) и получаем

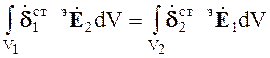                                                                    (3.18)

За пределами объемов V₁ и V₂ источники  соответственно отсутствуют и поэтому интегрирование в (3.18) производится только по V₁ и V₂.

Выражение (3.18), представляющее частный случай леммы Лоренца, называется теоремой взаимности. Рассмотрим пример применения теоремы взаимности к задаче передачи энергии между двумя антеннами.

Пусть антенны представляют собой проводники длиной l₁ и l₂, длиной значительно меньшей длины волны, по которым протекают токи, равномерно распределенные по их длине с плотностями  рис.3.4. Токи возбуждают в бесконечном объеме V электромагнитные поля . Объемы проводников V₁=l₁DS₁; V₂ = l₂DS₂. Полные сторонние токи в антеннах

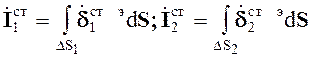.                                                        (3.19)

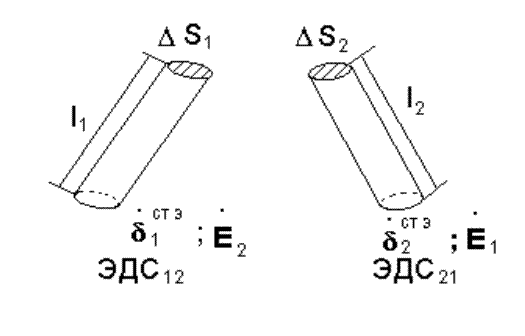
Рис. 3.4 Взаимодействие двух антенн

С учетом (3.19) теорему взаимности (3.18) можно записать в виде

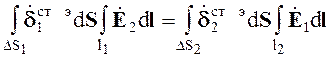                                                    (3.20)

или   ЭДС₁₂ =   ЭДС₂₁ последнее выражение запишем в виде

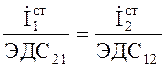,                                                                              (3.21)

где ЭДС₁₂ - электродвижущая сила, наводимая полем антенны 2 в антенне 1, ЭДС₂₁ - электродвижущая сила, наводимая полем антенны 1 в антенне 2.

Отношение тока в первой антенне к наводимой им ЭДС во второй антенне равно отношению тока во второй антенне к наводимой им ЭДС в первой антенне.

Считая одну из антенн передающей, а другую приемной, видим, что передающая антенна, возбуждаемая током , вызывает появление в приемной антенне той же ЭДС, которую в передающей антенне вызвал бы такой же величины ток возбуждающий приемную антенну.

Вывод. Характеристики приема - передачи не изменяются при взаимной замене антенн.

ГЛАВА 4

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Понятие волны одно из важнейших общих понятий физики. Под волной понимают процесс, приводящий к передаче энергии при постепенном вовлечении среды в этот процесс.

Волновые гармонические процессы характеризуются следующими параметрами: амплитудой, частотой, фазой, поляризацией, фазовым фронтом волны, длиной волны.