Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 30

Рис. 6.1 Продольно-однородные структуры а) - прямоугольный волновод, б) - круглый волновод, в) - коаксиальная линия, г) - диэлектрический круглый волновод, д) - двухпроводная линия, е) - диэлектрический прямоугольный волновод, ж) - несимметричная полосковая линия, з) - щелевая линия.

Запишем волновое однородное уравнение используя метод комплексных амплитуд, то есть уравнение для гармонических колебаний, в котором временная зависимость имеет вид . Это уравнение при исключении временного множителя принимает вид

                                                     (6.1)

и называется однородным уравнением Гельмгольца.

Применим к уравнению (6.1) метод разделения переменных. Для этого предположим что (x, y, z) можно представить в виде произведения двух неизвестных функций разных аргументов

                                      (6.2)

Подставляя (6.2) в (6.1) получим:

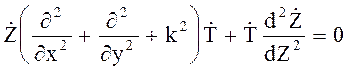                                (6.3)

Разделим все члены на  и введем оператор

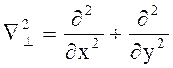                                                   (6.4)

Теперь получим

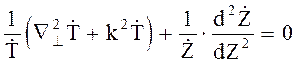                                         (6.5)

В выражении (6.5) произошло разделение переменных. Первый член зависит от x, y и не зависит от z; второй - зависит от z и не зависит от x, y. Поэтому при изменении z первый член сохраняет постоянное значение, так как производная от него по z равна нулю.

Можно сделать вывод, что второй член равен некоторой константе. Обозначим ее g² . Для сохранения равенства (6.5) при этом следует приравнять первый член к величине -g² .

Теперь получаем два независимых уравнения

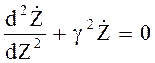                                                      (6.6)

                                         (6.7)

В экспоненциальной форме решение первого уравнения имеет вид

, где  и  - подлежащие определению постоянные.

Поэтому

                         (6.8)

Два члена выражения (6.8) - комплексные амплитуды волн, величина g называется постоянной распространения, а также продольным волновым числом.

Для того чтобы уравнение Гельмгольца в виде (6.5) имело определенное решение, необходимо поставить краевую (граничную) задачу.

Первая краевая задача для краевого уравнения Гельмгольца, при которой решение  ищется внутри области, ограниченной контуром L_^

  на  L_^                                  (6.9)

Задача имеет бесконечно множество решений, каждое из которых получается при определенном значении параметра c. Решения Т_n называются собственными функциями, а соответствующие им значения  параметра c - собственными значениями. Нумерация производится в порядке не убывания собственных значений

Если разным собственным функциям соответствуют одинаковые собственные значения, то последние называются вырожденными.

Вторая краевая задача для двумерного уравнения Гельмгольца

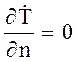       на L_^,                                 (6.10)

при которой решение  также ищется внутри области, ограниченной контуром L_^. Здесь производная берется по нормали к контуру n₀.

Решение этой задачи также дает систему собственных функций, которые отвечают собственным значениям.

Как для первой так и для второй задачи можно получить следующее соотношение

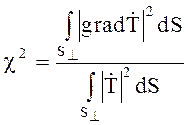.                                                (6.11)

Из (6.11) следует, что собственные значения рассматриваемых задач неотрицательны.

Если рассматриваются несколько подобластей (рис.6.1. д, е, ж, з) и для каждой из них k принимает свое значение k_i, то соответственно в (6.5) возникают разные поперечные волновые числа

                                               (6.12)

Постоянная распространения g является общей для всей структуры.

Любая компонента  и  электромагнитного процесса в продольно-однородной структуре может быть представлена в виде (6.8). Будем рассматривать волны одного направления, для чего положем . Векторы  и  выразим как

;                                  (6.13)

Поставляя (6.12) в однородные векторные уравнения Гельмгольца, получим

,  ,                               (6.14)

где  .

Причем, если имеется несколько однородных областей i с различными свойствами, то столько же раз пишутся уравнения и