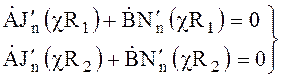 (6.61)
(6.61)
Или, записывая определитель системы
(6.61), получаем уравнение для определения ![]()
![]() , (6.62)
, (6.62)
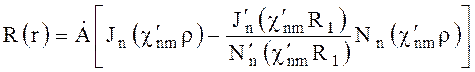 , (6.63)
, (6.63)
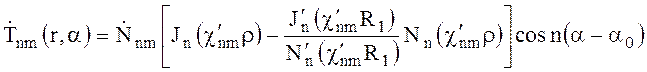 (6.64)
(6.64)
6.4. Волны в прямоугольном волноводе
Наибольшее применение среди полых металлических волноводов находит прямоугольный волновод, показанный на рис. 6.8.
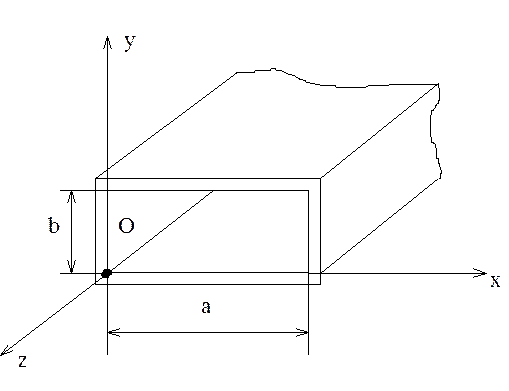
Рис. 6.8. Прямоугольный волновод
В прямоугольном волноводе с идеально проводящими стенками могут существовать только волны типа Е и Н.
Для определения
продольной составляющей ![]() для волн типа Е используют
решение первой краевой задачи так как
для волн типа Е используют
решение первой краевой задачи так как ![]() = 0 при
х = 0; у= 0; х= а; у = b.
= 0 при
х = 0; у= 0; х= а; у = b.
Для определения
продольной составляющей ![]() используем решение
второй краевой задачи
используем решение
второй краевой задачи 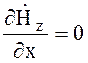 при х = 0 и х = а;
при х = 0 и х = а; 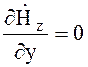 при у = 0 и у = b. Поперечные составляющие
можно найти из выражений (6.15).
при у = 0 и у = b. Поперечные составляющие
можно найти из выражений (6.15).
Запишем эти выражения в
декартовой системе координат в развернутом виде. При определении поперечных
составляющих Е - волн следует учесть, что в (6.65) ![]() , а при
определении поперечных составляющих для Н - волн -
, а при
определении поперечных составляющих для Н - волн - ![]() .
.
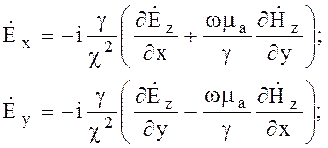
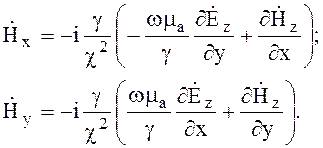 (6.65)
(6.65)
Е - ВОЛНЫ
Согласно (6.36) и (6.37)
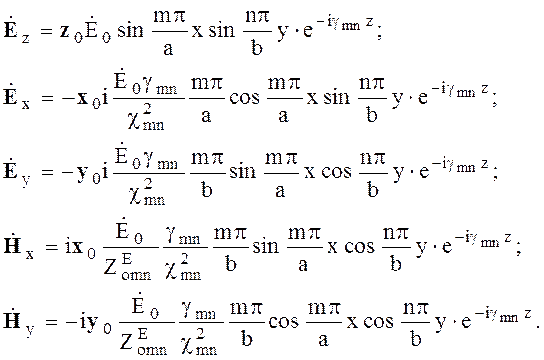 (6.66)
(6.66)
Здесь ![]() -
характеристическое сопротивление для Е - волн.
-
характеристическое сопротивление для Е - волн.
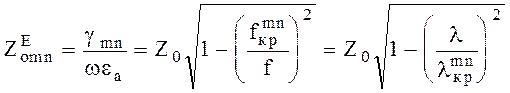 , (6.67)
, (6.67)
где Z0 = 120p,
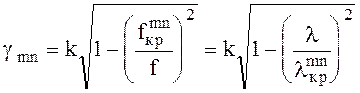 , (6.68)
, (6.68)
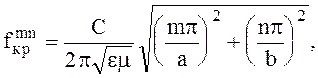 (6.69)
(6.69)
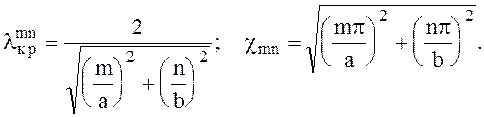 (6.70)
(6.70)
Здесь fкр - наименьшая частота, начиная с которой волна распространяется по волноводу.
Из (6.69) видно, что наименьшую критическую частоту среди Е - волн в прямоугольном волноводе имеет волна Е11 (m = 1, n = 1). Критическая длина волны Е11 наибольшая из Е - волн
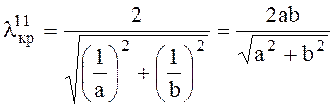 (6.71)
(6.71)
Фазовая скорость
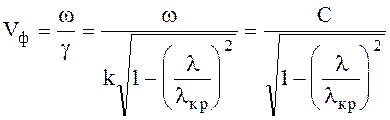 ; (6.72)
; (6.72)
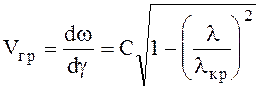 (6.73)
(6.73)
Н - ВОЛНЫ
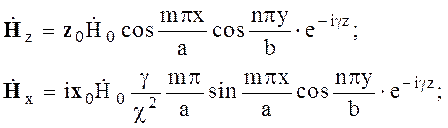
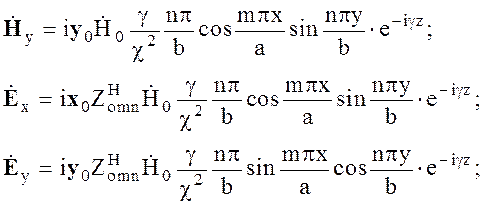 (6.74)
(6.74)
где 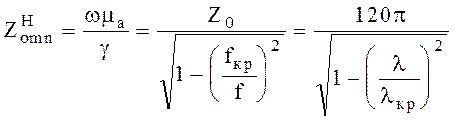 (6.75)
(6.75)
Остальные параметры волн Нmn выражаются теми же формулами, что и соответствующие параметры волн Еmn формулами (6.68) ... (6.73).
Полученные решения показывают что в прямоугольном волноводе может существовать бесконечное число волн Е и Н, которые определяются числами m и n.
Каждому типу волны Еmn и Hmn соответствуют свои параметры и своя структура поля.
Под структурой поля волны в волноводе понимают показанное в виде векторных линий распределение составляющих поля Е и Н в фиксированный момент времени t = t0. Касательная к векторной линии в точке показывает направление вектора поля в данной точке. Число силовых линий, пересекающих единичную площадку, расположенную перпендикулярно направлению вектора в данной точке показывает относительную величину вектора. На рис. 6.9 показана структура волны Е11.
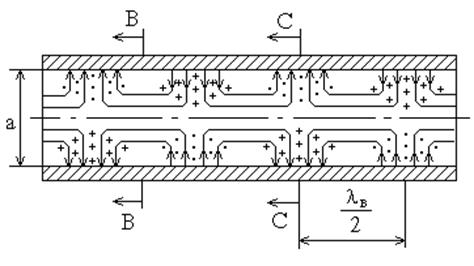
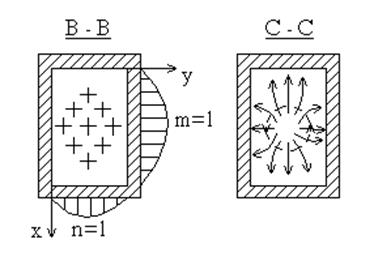
Рис. 6.9. Структура волны Е11 в прямоугольном волноводе.
На рис. 6.9 показано
сечение волновода В-В, в котором распределение амплитуды продольной
составляющей вектора электрического поля Еz подчиняется
закону 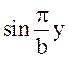 вдоль оси у (m = 1, n= 1). Вдоль оси х
имеется одна стоячая полуволна (m = 1) с поперечным волновым числом
вдоль оси у (m = 1, n= 1). Вдоль оси х
имеется одна стоячая полуволна (m = 1) с поперечным волновым числом 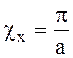 и вдоль оси у также одна стоячая полуволна
с поперечным волновым числом
и вдоль оси у также одна стоячая полуволна
с поперечным волновым числом 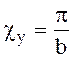 . Из выражений (6.68) и
(6.74) можно сделать вывод, что индексы m и n показывают количество стоячих
полуволн по широкой и узкой стенкам волновода в картине распределения амплитуд
составляющих поля. Каждый тип волны имеет свою критическую частоту (6.69),
значение которой зависит от размеров волновода а и b и индексов m и n.
Наименьшую критическую частоту (наибольшую критическую длину волны) имеет волна
Н10 (m = 1, n = 0). При повышении частоты она первой возбуждается в
прямоугольном волноводе. При дальнейшем увеличении частоты дополнительно к
волне Н10 в волноводе возбуждаются волны Н20, Н01,
Н21, Е11, Н21, Н21 и т. д. Если по
оси длин волн отложить значения критических длин волн различных типов, то
получим диаграмму, показанную на рис. 6.10, которая называется диаграммой типов
волн.
. Из выражений (6.68) и
(6.74) можно сделать вывод, что индексы m и n показывают количество стоячих
полуволн по широкой и узкой стенкам волновода в картине распределения амплитуд
составляющих поля. Каждый тип волны имеет свою критическую частоту (6.69),
значение которой зависит от размеров волновода а и b и индексов m и n.
Наименьшую критическую частоту (наибольшую критическую длину волны) имеет волна
Н10 (m = 1, n = 0). При повышении частоты она первой возбуждается в
прямоугольном волноводе. При дальнейшем увеличении частоты дополнительно к
волне Н10 в волноводе возбуждаются волны Н20, Н01,
Н21, Е11, Н21, Н21 и т. д. Если по
оси длин волн отложить значения критических длин волн различных типов, то
получим диаграмму, показанную на рис. 6.10, которая называется диаграммой типов
волн.
Диаграмма типов волн показывает какие волны одновременно существуют при заданной длине волны и выбранных размерах волновода.
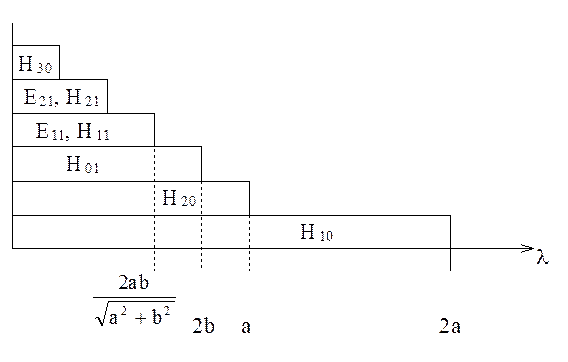
Рис. 6.10. Диаграмма типов волн в прямоугольном волноводе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.