Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 42

Как видно из рис. 6.28 и 6.29, МПЛ состоит из двух элементарных ячеек. Решение задачи сводится к интегрированию уравнений Гельмгольца для  каждой  из  частичных  областей,  входящих в рассматриваемую ячейку

, где  или  - продольные составляющие напряженности электрического или магнитного поля,  - поперечные волновые числа. На границах областей 1 и 2 должны быть заданы граничные условия: касательная составляющая  на электрических стенках; касательная составляющая  на магнитных стенках; на границе раздела сред касательные составлщие , , то есть они непрерывны. Кроме этого должны выполняться условия Мейкснера на ребрах полоскового проводника, толщина которого считается бесконечно малой.

Решение поставленной таким образом задачи [3] позволяет получить дисперсионные уравнения, показывающие зависимость относительной постоянной распространения коэффициента замедления  от частоты, выражения для составляющих полей в МПЛ, рассмотреть влияние экрана и ширины полоски на различные типы волн.

Хотя сама задача поставлена строго, но полученное решение в виде бесконечных рядов, оказывается громоздким и приближенным за счет ограничения числа членов ряда.

Для анализа используется ЭВМ. Проведенный машинный анализ решения позволяет сделать следующие выводы [4], [5].

Волны, передаваемые по МПЛ, являются гибридными. Это касается и низшей основной волны в МПЛ, которая аналогична ТЕМ-волне в двухпроводной линии. Критическая частота этой волны f_кр = 0. Однако в ней поперечные компоненты значительно преобладают над продольными.

Влияние экрана на дисперсионные характеристики МПЛ сильно сказывается только при его близком расположении к полосковому проводнику. При значениях а/w > 20 и у₂ / у₁ > 20 он практически не влияет на дисперсионные характеристики как основной, так и высших типов волн. Это позволяет в качестве модели открытых МПЛ брать модели, полученные для экранированных структур.

При w/a = 0 экранированная МПЛ превращается в двухслойный волновод, в котором отсутствует квази-ТЕМ волна.

При w/a ® 0 сказывается сильное влияние зазоров между экраном и полоском на дисперсионную характеристику квази-ТЕМ волны.

Высшие типы волн при a/w >> 1 практически не изменяются при уменьшении ширины полоска и даже при его отсутствии. Они определяются параметрами двухслойного волновода, образующегося при удалении полоска. Эти волны называются экранными.

Кроме экранных волн в рассматриваемой МПЛ могут существовать так называемые подполосочные волны. Поля этих волн концентрируются в основном над полосковым проводником. Эти волны сильно зависят от размера полоскового проводника. Деление волн на экранные и подполосочные является условным. Волна одного и того же типа при малых w/a может быть экранной, а при больших w/a подполосочной. Основная волна в МПЛ - квази-ТЕМ волна. Поэтому она представляет особый интерес в практических разработках интегральных микросхем СВЧ.

Основными параметрами волны ТЕМ являются: волновое сопротивление, длина волны, затухание, передаваемая мощность.

Кроме того, вводятся параметры, учитывающую дисперсию квази-ТЕМ волны: коэффициент замедления, эквивалентная диэлектрическая проницаемость, граничная частота и предельная частота.

Волновое сопротивление МПЛ будем выражать как

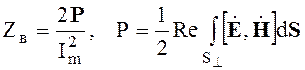,                                      (6.167)

где P - средняя передаваемая мощность, I_m - полный ток полоскового проводника.

Также можно определить волновое сопротивление как

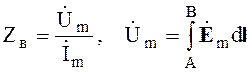                                                (6.168)

Обе формулы дают близкое значение: когда толщина подложки значительно меньше длины волны в ее диэлектрике.

Волновое сопротивление в соответствии с определением (6.167) можно рассчитать по формуле [3]

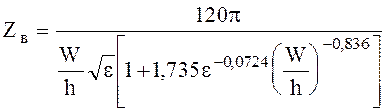                          (6.169)

В квазистатическом приближении до граничной частоты, определяющую частоту, выше которой следует учитывать дисперсию

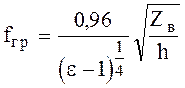,                                                          (6.170)

где w - ширина полоска, h - толщина подложки, e - относительная диэлектрическая проницаемость подложки, Z_в, [Ом] - волновое сопротивление МПЛ в квазистатическом приближении.