В первом случае за счет убывания энергии в объеме V происходит ее излучение за пределы объема. Второе соотношение не обязательно говорит об изоляции объема V. В одной части поверхности S поток вектора может быть положительным, а в оставшейся части отрицательным, а суммарный поток через всю замкнутую поверхность RS = 0. В последнем случае потери и запас энергии в объеме V покрываются за счет поступающей извне в объем энергии RS <0.
Выражение (2.65) характеризует баланс энергии в дифференциальном виде и может быть записано в виде
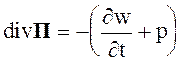 (2.74)
(2.74)
Возможны следующие варианты обмена энергий между точками, расположенными на дифференциально малом расстоянии
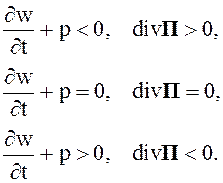 (2.75)
(2.75)
В первом случае энергии в рассматриваемой точке убывает за счет ее излучения в соседнюю точку пространства. Второе выражение показывает процесс передачи энергии через рассматриваемую точку, не нарушая запас энергии в точке. Последнее соотношение соответствует поступлению энергии в рассматриваемую точку в любой заданный момент времени.
Если в точке отсутствует переход энергии электромагнитного поля в другие виды энергии (p = 0), то уравнение баланса принимает вид
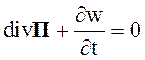 (2.76)
(2.76)
Первый член характеризует движение энергии, а второй - запас энергии в точке.
Уравнение (2.76) по форме аналогично уравнению непрерывности
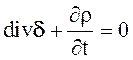 (2.77)
(2.77)
Конвекционный ток можно представить как движение зарядов со скоростью v
d = rv (2.78)
Аналогично можно записать и вектор Пойтинга из (2.76) как
П = wvэ (2.79)
где Vэ - скорость переноса энергии, следовательно
vэ = П / w (2.80)
Уравнение баланса для средней за период энергии
Наибольший интерес представляют энергетические соотношения для средних за период значений величин. Средним значением величины периодической функции считают
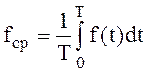 (2.81)
(2.81)
При применении метода комплексных векторных амплитуд замена действительных векторов представляющими их комплексными векторами правомерна только в тех выражениях, в которые векторы входят линейно, то есть над ними производятся линейные операции: сложение, вычитание, умножение и деление на действительную величину.
При наличии нелинейных операций (умножения и деления) действительная часть произведения или частного комплексных чисел не равна произведению действительных частей комплексных сомножителей или частному действительных частей комплексных чисел
![]() (2.82)
(2.82)
Здесь F1, F2 - произвольные
векторные функции, ![]() - соответствующие F1 и F2 комплексные функции,
то есть функции, действительные части которых равны F1 и F2 соответственно.
- соответствующие F1 и F2 комплексные функции,
то есть функции, действительные части которых равны F1 и F2 соответственно.
Применение комплексных скалярных и векторных функций в нелинейных операциях возможно при представлении с их помощью действительных функций в виде
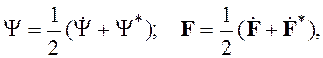 (2.83)
(2.83)
где ![]() и
и ![]() -
функции, комплексно сопряженные с
-
функции, комплексно сопряженные с ![]() и
и ![]() .
.
Определим среднее значение вектора Пойтинга через его комплексное значение, применяя представление Е и Н в виде (2.83)
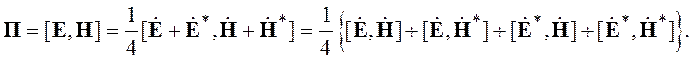 (2.84)
(2.84)
Здесь векторы
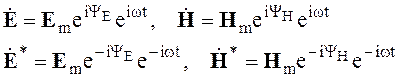 (2.85)
(2.85)
Из выражений (2.84) и (2.85) получаем
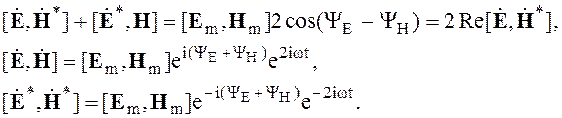 (2.86)
(2.86)
Следовательно,
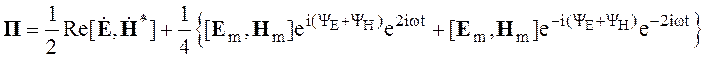 (2.87)
(2.87)
Найдем среднее значение вектора Пойтинга
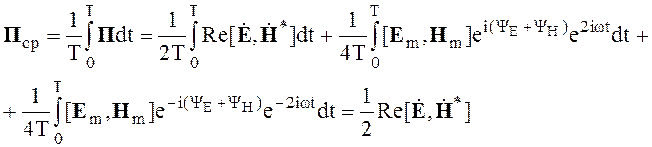 (2.88)
(2.88)
Последние два интеграла равны нулю, так как в них производится интегрирование периодических функций по периоду Т.
Комплексный вектор
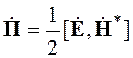 (2.89)
(2.89)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.