Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 4

S = S n₀,                                                        (1.31)

где S - величина площади, n₀ - единичный вектор, направленный перпендикулярно к площадке и показывающий ее ориентацию в пространстве.

Запишем теперь отношение циркуляции по замкнутому контуру С вектора F к величине площади S, охватываемой контуром при S ® 0

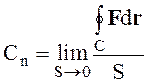                                                       (1.32)

Значок n у величины С_n означает, что величина C_n зависит от ориентации площадки . При каком-то положении  = n₀ значение С_n будет максимальным.

При значении C_n при n₀ вводится векторная величина

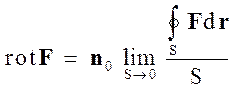                                         (1.33)

которая называется ротором (вихрем) векторного поля F.

Для всякого потенциального поля F = grad j

rot grad j = 0                                                                    (1.34)

Поэтому потенциальные поля называются также безвихревыми.

Поля, для которых div F = 0, называются  соленоидальными. Поэтому векторное поле rot V = F соленоидальное, так как

div rot V = 0                                                                      (1.35)

Потенциальные поля F (для которых rot F = 0) могут быть одновременно и соленоидальными (div F = 0). Такие поля называются гармоническими.

Важнейшая теорема, связанная с понятием ротора, есть теорема Стокса, устанавливающая связь между линейным и поверхностным интегралом.

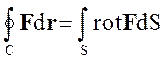                                                     (1.36)

Циркуляция вектора по замкнутому контуру равна потоку ротора вектора через поверхность, ограниченную данным контуром.

Из теоремы Стокса непосредственно следует, что

rot grad j = 0                                                          (1.37)

Из формулы Остроградского-Гаусса (1.28) можно получить выражение

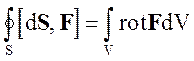                                                (1.38)

В векторном анализе очень часто применяется дифференциальный оператор Гамильтона (набла), который в декартовой системе координат определяется как

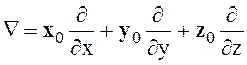                                       (1.39)

Применение оператора оказывается очень удобным во многих вопросах векторного анализа.

Рассматривая вектор grad j, можно записать

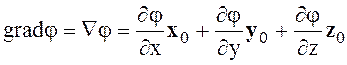                                (1.40)

Дивергенцию вектора F можно записать как скалярное произведение

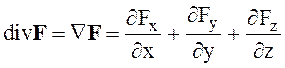                                           (1.41)

Ротор вектора F можно записать как векторное произведение

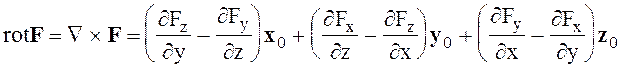          (1.42)

Скалярное произведение Ñ * Ñ обозначается как

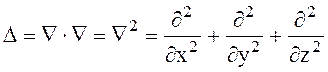                                   (1.43)

И называется оператором Лапласа, а уравнение

D j  = 0                                                                   (1.44)

уравнением Лапласа.

1.3. Комплексные числа и действия над ними. Функции комплексного переменного

Комплексным числом называется число вида

z = x + iy,                                                                (1.45)

где х и y - действительные числа, а i - символ, называемый мнимой единицей.

Число вида z = x + i0 считается действительным, число z = 0 + iy мнимым.

Числа x и y называются соответственно действительной (или вещественной) и мнимой частями числа z и обозначаются

x = Re z ;   y = Im z 

Комплексное число z = x - iy называется сопряженным по отношению к числу z = x + iy.

Если рассматривать действительные числа x и y как декартовы координаты точки М на плоскости х0у (рис. 1.10), то точка М будет геометрическим изображением комплексного числа z.

Введем радиус-вектор OМ точки М

r = OM.

Длина радиус-вектора r называется модулем или абсолютной величиной комплексного числа z и обозначается r = ½z½

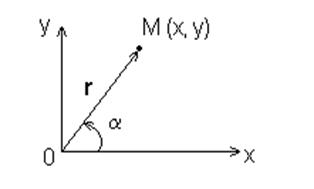
Рис. 1.10. Геометрическое изображение комплексного числа.

Угол a между радиус-вектором r и положительным направлением оси Oх, отсчитываемый от оси Oх, называется аргументом комплексного числа z и обозначается a = Arg z. Аргумент комплексного числа определен неоднозначно, с точностью до слагаемого, кратного 2 p.

Из всех значений комплексного числа особо выделяется главное значение, обозначаемое arg z и удовлетворяющее неравенству

- p < arg z < p

Модуль и аргумент связаны с действительной и мнимой частью соотношениями