(6.135)
из-за возможности возникновения волны Н11.
Здесь lд - длина волны в диэлектрике, заполняющим линию. Поэтому будет ограничена и предельная мощность. Из (6.135) следует
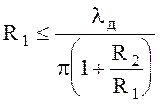(6.136)
Из (6.134) и (6.136) имеем
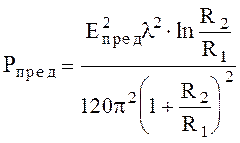(6.137)
Затухание в коаксиальной линии передачи, обусловленное потерями на поверхности центрального проводника и внутренней поверхности внешнего проводника, можно определить с помощью выражения (6.85)
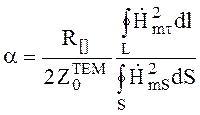(6.138)
Принимая в (1.138) dS = r × dr × da, HmS = C/r (здесь C - константа), Нmt = C/R2 и dl = R2 × dj для окружности внешнего проводника и C/R1 и R1× dj для окружности внутреннего проводника, получим
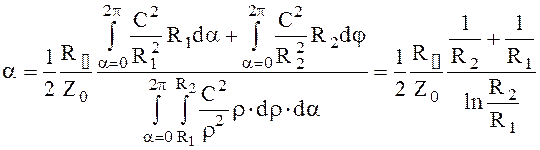(6.139)
Выбор размеров коаксиальной линии передачи производится, исходя из следующих требований: обеспечения необходимого рабочего диапазона, обеспечения передачи больших мощностей, обеспечения малого затухания. Для выполнения первого требования достаточно выбрать радиус R1 в соответствии с условием (6.136), задаваясь соотношением R2 / R1. Если требуется минимальное затухание в линии a мин., то исследуем выражение (6.112) на минимум.
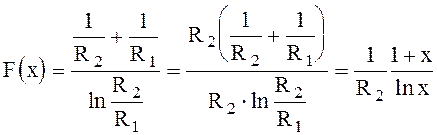
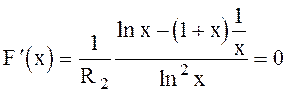
или, так как ln2 x ¹ 0 при R2 / R1 ¹ 1, получаем
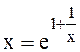(6.140)
Решение (1.140) дает х = 3,591, то есть отношение
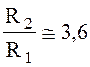
Подставляя отношение 3,6 в (6.136), получаем для случая наименьших потерь
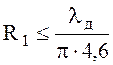(6.141)
Волновое сопротивление
Zв = 60 × ln(R2 / R1) = 76,85 » 77 Ом. (6.142)
Если требуется передать по линии максимальную мощность, то исследуется на максимум выражение (6.137).
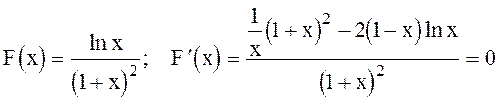
так как знаменатель не равен нулю, получаем
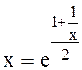
Решение дает х = R2 / R1 = 2,093 » 2,1.
Выражение (6.136) принимает вид
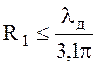(6.143)
Волновое сопротивление
Zв = 60 × ln(R2 / R1) = 44,32 » 44 Ом. (6.144)
Стандартные коаксиальные линии передачи имеют, соответственно, волновые сопротивления 75 Ом и 50 Ом.
6.7. Диэлектрические волноводы
Известно много различных видов диэлектрических волноводов: чисто диэлектрические неэкранированные, металлодиэлектрические неэкранированные, металлодиэлектрические частично экранированные и экранированные рис. 6.22.
Если граница раздела рассматриваемой однородной структуры представляет координатную поверхность, то в основе анализа лежит решение скалярного уравнения Гельмгольца, получаемое методом разделения переменных. В отношении других структур замкнутые выражения решений отсутствуют.
Круглый диэлектрический волновод
На рис. 6.23 показан диэлектрический круглый волновод и цилиндрическая система координат.
В диэлектрическом волноводе возможно существование волн НЕ, ЕН (гибридных волн), а также волн Е и Н.
В задаче отыскания типов волн в диэлектрическом волноводе следует учесть, что поле будет существовать как внутри его, так и снаружи. Поэтому продольные составляющие электрической и магнитной компонент поля внутри стержня должны удовлетворять уравнениям
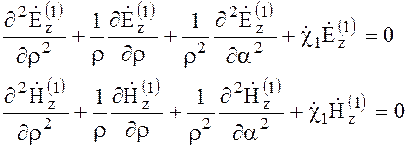, (6.145)
где 
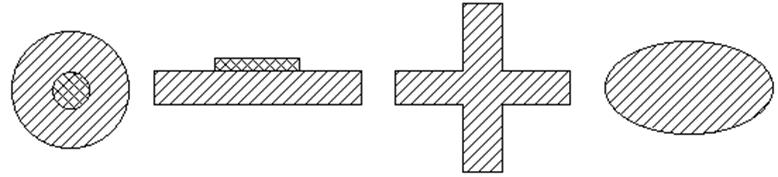
Диэлектрические неэкранированные волноводы
Металлодиэлектрические неэкранированные
Металлодиэлектрические частично экранированые.
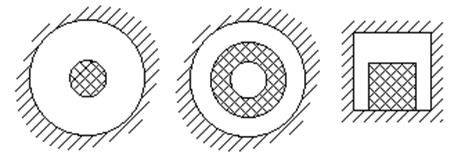
Металлодиэлектрические полностью экранированные.
Рис. 6.22. Диэлектрические волноводы.
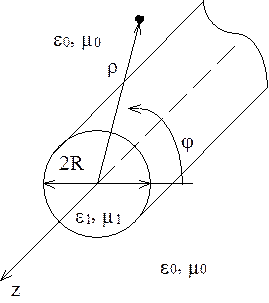
Рис. 6.23. Круглый диэлектрический волновод.
Вне диэлектрического стержня составляющие 
также удовлетворяют уравнениям
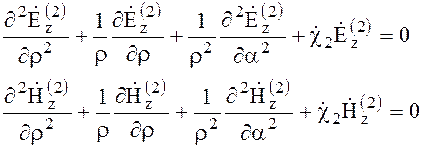(6.146)
где 
Общим решением уравнений (6.145) и (6.146) является линейная комбинация функций Бесселя и Неймана (6.48). Однако напряженность поля в любой внутренней точке диэлектрического волновода, в том числе и в его центре (r = 0), должна быть конечной, поэтому функции Неймана следует исключить из решения и при r £ R.
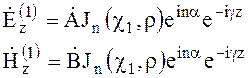(6.147)
Вне цилиндра, где структура поля соответствует структуре
поверхностной волны, амплитуда полей должна убывать по экспоненциальному
закону. Этому требованию удовлетворяет функция Ханкеля от чисто мнимого аргумента
. Поэтому решение уравнений (6.146)
записывается в виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.