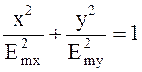Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 23

                                                                                     (4.93)

с параметрами

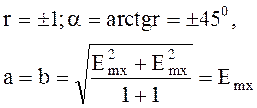                                                        (4.94)

Выражение описывает вектор Е волны с круговой поляризацией имеет вид

E = E_mx [x₀ cos(wt - kz + j) ± y₀ sin(wt - kz + j)]                                  (4.95)

Линейная поляризация. Векторы E_mx x₀ и E_my y₀ имеют произвольные значения амплитуд, f = 0. При этих условиях выражение (4.87) принимает вид

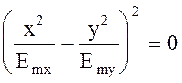               или 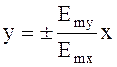                                                                   (4.96)

Это уравнение прямой.

Параметры

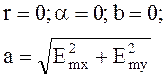                                                    (4.97)

Выражение для  вектора Е при линейной поляризации принимает вид

E = (x₀E_mx ± y₀E_my) cos(wt - kz - j)                                            (4.98)

Составляющие  вектора  Е  находятся  в  фазе, поэтому можно всегда найти геометрическую сумму векторов x₀E_mx + y₀E_my в виде . Здесь  образуется поворотом системы координат x, y на угол равный

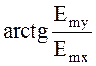                                                                (4.99)

4.8. Волны в гиротропной среде

Если среда анизотропная, то ее свойства различны для волн противоположных направлений и для таких сред не справедлива теорема взаимности. Невзаимные устройства широко применяются в технике. Для их реализации используют наиболее часто анизотропные магнетики - ферриты. Ферриты составляют группу ферромагнитных веществ, обладающих очень малой проводимостью и названных поэтому магнитодиэлектриками.

Под воздействием постоянного внешнего магнитного поля Н₀ происходит ориентация моментов доменов в феррите, которые выстраиваются параллельно вектору Н₀ . При этом феррит приобретает значительную намагниченность. Максимальная намагниченность данного материала - намагниченность насыщения соответствует одинаковой ориентации всех доменов. В зависимости от состава и условий изготовления феррита, то есть его марки М_нас = 30...500 кА/м. В больших пределах меняется и начальная магнитная проницаемость ферритов (в слабых полях) m_нач = 10 ... 3000. На сверхвысоких частотах используются ферритовые элементы намагниченные постоянным магнитным полем Н₀ (обычно до насыщения). В этом состоянии феррит анизотропен по отношению к высокочастотному электромагнитному полю.

Намагниченный феррит представляет собой гиротропную среду, свойства которой описываются с помощью тензора магнитной проницаемости

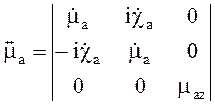                                            (4.100)

Для решения задачи по распространению волн в гиротропной среде запишем уравнения Максвелла в декартовой системе координат

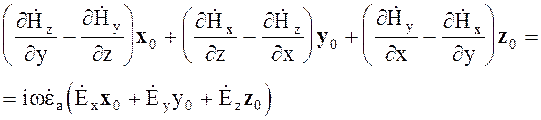                    (4.101)

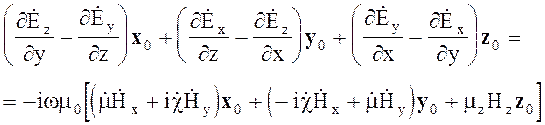                   (4.102)

Приравнивая члены при соответствующих ортах, получим систему скалярных уравнений

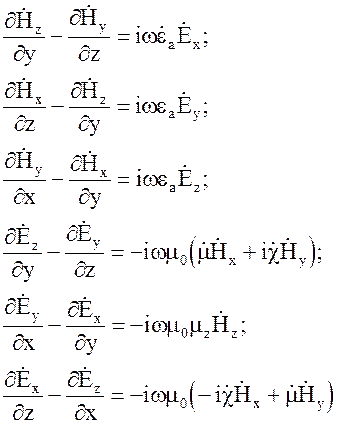                                            (4.103)

Решение системы уравнений в виде (4.103) обычно не производят, так как на практике в основном применяются продольное и поперечное намагниченные ферриты.

Распространение плоской однородной волны вдоль оси z (в направлении намагничивания феррита H₀  = H_z z₀.

В этом случае значения производных по x и y

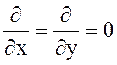
Значение производной по z

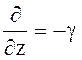
где - g = ib + a постоянная распространения, значение которой требуется найти.

Система уравнений (4.103) упрощается и принимает вид

                           (4.104)

                  (4.105)

Из уравнений (4.104) получаем

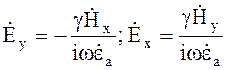                                                    (4.106)

Заменим в (4.105)  в соответствии с (4.106) и получим

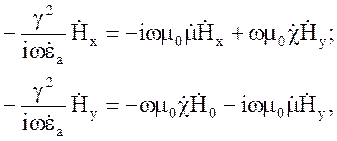                                            (4.107)

или 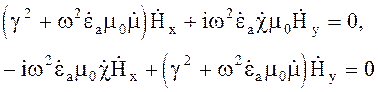                                                  (4.108)

Записывая  и  получим из (4.108)

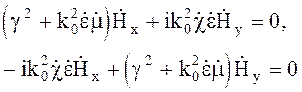                                        (4.109)

Здесь - относительные значения параметров.

Однородная система уравнений (4.109) имеет решения только при равенстве нулю ее определителя или 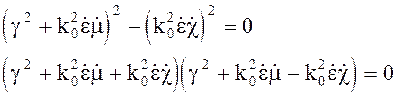                                               (4.110)

Из последнего выражения получаем два решения

                                       (4.111)

Можно сделать вывод, что при распространении однородной плоской волны вдоль оси z в гиротропной среде она распадается на две с разными постоянными распространения. Подставляя значение из (4.111) в (4.109), получаем