Составляющая Еу изменяется вдоль оси х по
закону 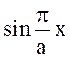 , вдоль оси у остается постоянной. Поэтому
наибольшая плотность векторных линий Еу в центре поперечного
сечения волновода при x = а / 2 и наименьшая у боковых стенок.
, вдоль оси у остается постоянной. Поэтому
наибольшая плотность векторных линий Еу в центре поперечного
сечения волновода при x = а / 2 и наименьшая у боковых стенок.
Вектор Н имеет две составляющие Нх и
Нz. Составляющая Нх изменяется по закону 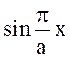 , аналогично Еу, а составляющая
Нz по закону
, аналогично Еу, а составляющая
Нz по закону 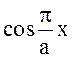 . Вдоль оси у обе
составляющие вектора Н остаются постоянными.
. Вдоль оси у обе
составляющие вектора Н остаются постоянными.
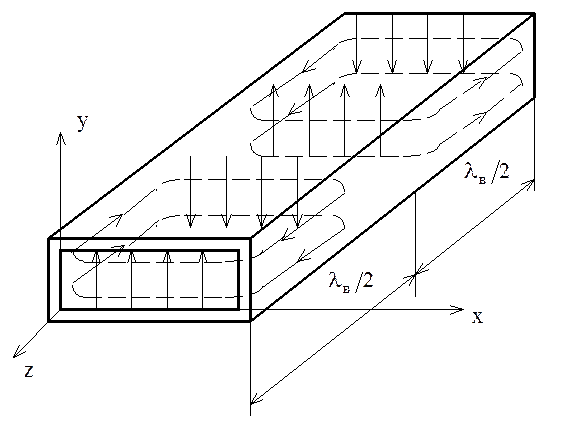
Рис. 6.12. Структура волны Н10 в прямоугольном волноводе.
При проектировании щелевых антенн удобнее
рассматривать не структуру полей, а структуру высокочастотных токов
проводимости dпр и
электрического смещения ![]() . Картина распределения
тока смещения,
. Картина распределения
тока смещения,
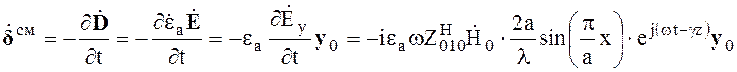 (6.88)
(6.88)
Как видно из (6.88) и (6.76), повторяет картину распределения
вектора электрического поля ![]() . Во времени ток
смещения как емкостной ток опережает электрическое поле на четверть периода
. Во времени ток
смещения как емкостной ток опережает электрическое поле на четверть периода ![]() . Об этом говорит множитель -i, на который
отличается выражение (6.88) от (6.86). При движении волны по стенкам волновода
текут поверхностные токи
. Об этом говорит множитель -i, на который
отличается выражение (6.88) от (6.86). При движении волны по стенкам волновода
текут поверхностные токи
![]() (6.89)
(6.89)
которые замыкаются через токи смещения. Токи текут по замкнутым контурам, поэтому токи проводимости в центральной вертикальной плоскости симметрии волновода замыкаются через токи электрического смещения. Векторные линии магнитной составляющей поля замыкаются вокруг токов электрического смещения.
Картина распределения токов в прямоугольном волноводе показана на рис. 6.13.
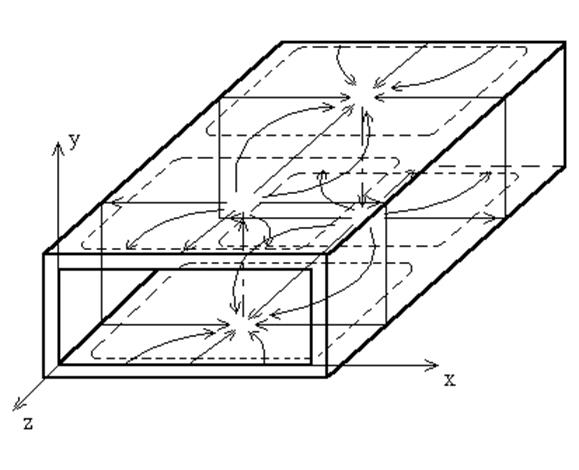
Рис. 6.13. Картина распределения токов для волны Н10 в прямоугольном волноводе.
Если в стенках волновода прорезать щели так, чтобы они разрывали векторные линии токов проводимости, то такие щели будут излучать. Если же щели не пересекают токи проводимости - излучение отсутствует. Например, щель, прорезанная вдоль волновода при х = а / 2 излучать не будет. Такая щель применяется в измерительной линии, где вдоль нее движется зонд (погруженный в волновод штырь малого диаметра).
В волноводе с волной Н10 существуют две плоскости, в которых вектор Н имеет круговую поляризацию.
Из выражений (6.76) видно, что вектор Н имеет
две составляющие, перпендикулярные друг другу - Нх и Нz.
Кроме того, следует, так как они отличаются на множитель 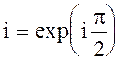 , что Нх и Нz
имеют разность фаз p/2. Если амплитуды Нх и Нz
будут равны, то вектор Н будет иметь круговую поляризацию. Из первого и
второго выражения (6.76) следует равенство амплитуд в виде
, что Нх и Нz
имеют разность фаз p/2. Если амплитуды Нх и Нz
будут равны, то вектор Н будет иметь круговую поляризацию. Из первого и
второго выражения (6.76) следует равенство амплитуд в виде
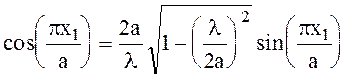 (6.90)
(6.90)
или
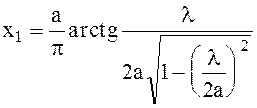 (6.91)
(6.91)
Таким образом, в плоскости х1 выполняются все три условия существования волны с круговой поляризацией вектора Н. В плоскости а-х1 вектор Н также имеет круговую поляризацию, только другого направления в результате того, что при а-х1 составляющая Нz меняет знак.
6.5. Волны в круглом металлическом волноводе
Круглый металлический волновод показан на рис. 6.14.
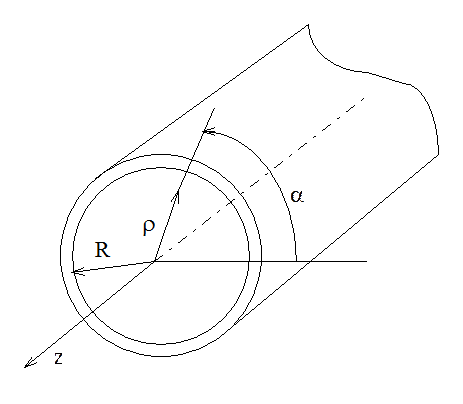
Рис. 6.14. Круглый металлический волновод
В круглом волноводе с идеально проводящими стенками могут существовать только Е-волны и Н-волны.
Для определения продольной составляющей Еz
для волн типа Е используем решение первой краевой задачи, так как ![]() при r = R.
при r = R.
Для определения продольной составляющей ![]() H-волн используем решение второй краевой
задачи, так как
H-волн используем решение второй краевой
задачи, так как 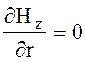 при r = R.
при r = R.
Поперечные составляющие можно найти из выражений (6.92).
При определении поперечных составляющих Е-волн следует учесть в (6.92), что Нz = 0, а при определении поперечных составляющих для Н-волн Еz = 0.
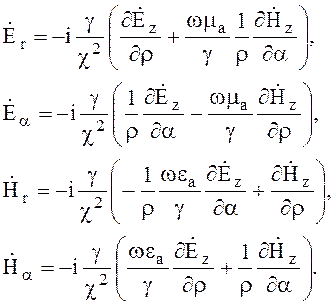 (6.92)
(6.92)
Е-волны
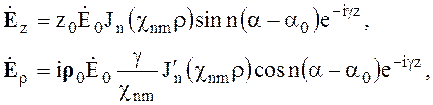
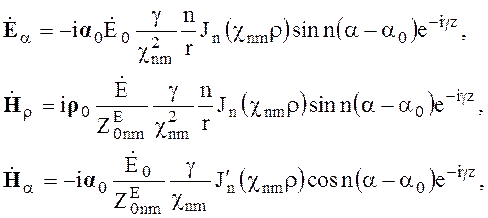 s (6.93)
s (6.93)
Здесь
для определения поперечных волновых чисел ![]() используется граничное условие для первой граничной
задачи (6.52),
используется граничное условие для первой граничной
задачи (6.52), ![]() . Значения корней уравнения
(6.52) Unm приводятся в таблице 6.1.
. Значения корней уравнения
(6.52) Unm приводятся в таблице 6.1.
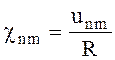 (6.94)
(6.94)
Критическая длина волны
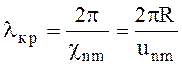 (6.95)
(6.95)
Характеристическое сопротивление
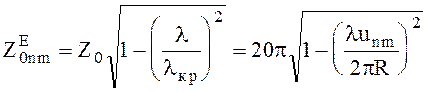 (6.96)
(6.96)
Постоянная распространения
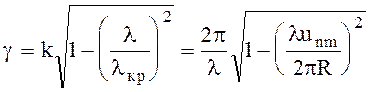 (6.97)
(6.97)
Длина волны в волноводе
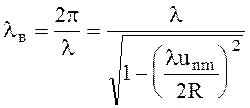 (6.98)
(6.98)
Критическая частота
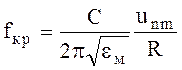 (6.99)
(6.99)
Фазовая скорость
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.