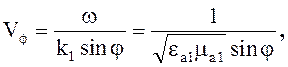Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 28

                                          (5.50)

Из соотношения

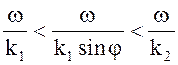
видно, что фазовая скорость больше скорости волны в среде 1, но меньше фазовой скорости в среде 2, так как k₁ sinj = k₂ sinq , а sinq >1, то есть k₂ < < k₁ sinj. Фазовая скорость уменьшается  при увеличении угла падения j.  Длина волны в среде 1

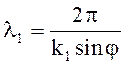                                                           (5.51)

Поверхность равных фаз y = const не совпадает с поверхностью равных амплитуд z = const. Следовательно, волна неоднородная. Распространяется волна вдоль поверхности раздела и поэтому называется поверхностной.

Поперечные составляющие векторов  и , перпендикулярные направлению распространения волны, находятся в фазе. Для волны с перпендикулярной поляризацией вектора  - это  и , для волны с параллельной поляризацией -  и .

Кроме поперечных составляющих поверхностные волны имеют продольные составляющие. При перпендикулярной поляризации падающей волны - , при параллельной поляризации - . В первом случае поверхностная волна называется Н - волной, во втором случае - Е - волной. Продольные составляющие всегда имеют сдвиг по фазе по отношению поперечных на 90°, на что указывает множитель “i”.

Амплитуды поперечных составляющих поверхностных волн при удалении от границы раздела в среде 1 по оси z изменяются по закону косинуса. Амплитуды продольных составляющих - по закону синуса.

Комплексный вектор Пойтинга

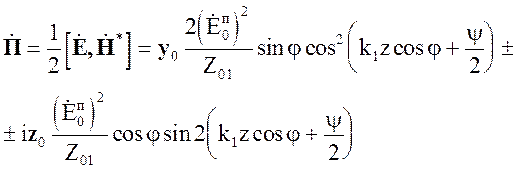                        (5.52)

Знак “+” соответствует случаю перпендикулярной поляризации, а знак “-” соответствует случаю параллельной поляризации.

Среднее значение вектора Пойтинга

                     (5.53)

Энергия переносится вдоль оси y

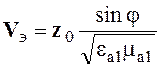                                                     (5.54)

Рассмотрим поле в среде 2. Воспользуемся для его рассмотрения общими выражениями полученными ранее для поля в среде 2. В случае перпендикулярной поляризация

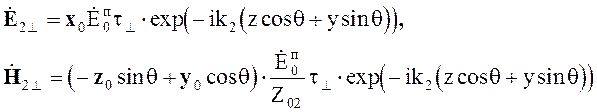          (5.55)

В случае параллельной поляризации

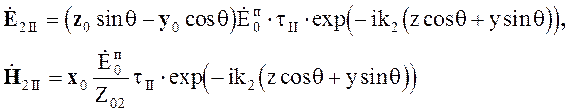               (5.56)

Обозначим , учтем, что , , 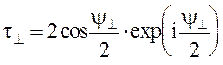, 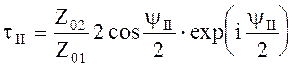получим

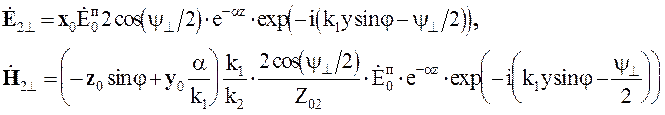          (5.57)

В случае параллельной поляризации

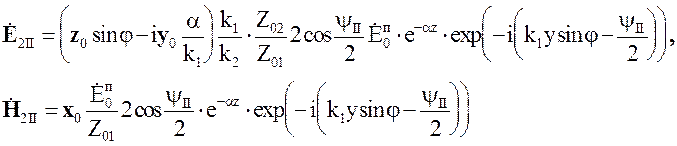          (5.58)

Из выражений (5.57) и (5.58) видно, что во второй среде поле имеет структуру плоской неоднородной волны, распространяющейся вдоль оси y. Поверхности равных фаз y = const и поверхности равных амплитуд z = const в этой волне взаимноперпендикулярны. Имеется продольная составляющая  при перпендикулярной поляризации падающей волны и продольная составляющая вектора  при параллельной поляризации падающей волны. Продольные составляющие векторов поля имеют сдвиг по фазе относительно поперечных на 90°. Вектор Пойтинга имеет две составляющие  и . Составляющая П_у чисто вещественная величина, составляющая П_z - чисто мнимая. Это означает, что во второй среде как и в первой энергия переносится вдоль оси y. Фазовая скорость волны такая же как и в первой среде. В направлении оси z амплитуды составляющих поля во второй среде уменьшаются по экспоненциальному закону , где 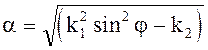  при j > j_кр.

Картина изменения поперечных и продольных составляющих поля поверхностной волны в среде 1 и среде 2 в плоскости равных фаз показана на рис.5.4.

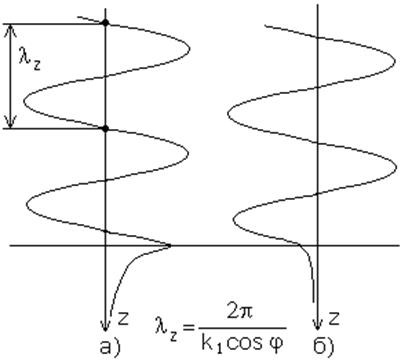
Рис. 5.4. Законы изменения амплитуды поперечных составляющих а) и продольных составляющих б) в поверхностной волне.

5.5. Поверхностные волны над идеально проводящей средой

Идеальный проводник характеризуется значением .

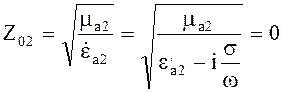                                           (5.59)

Следовательно,

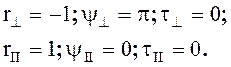                                          (5.60)

Выражения (5.60) справедливы при любом угле падения j. Поле во второй среде отсутствует. Поле в первой среде представляет собой поверхностную волну, распространяющуюся вдоль оси y.

                             (5.61)

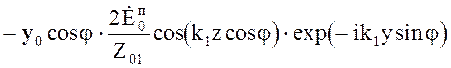
При параллельной поляризации падающей волны получаем

                            (5.62)

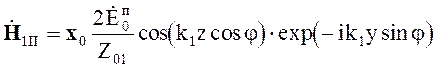
Фазовая скорость, длина волны и скорость переноса энергии определяются выражениями (5.50), (5.51), (5.54).

5.6. Стоячие волны

В случае нормального падения волны на идеально проводящую поверхность j = 0, следовательно, из (5.61) и (5.62) получаем

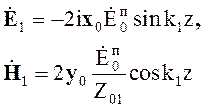                                                        (5.63)