Электротехника \ Техническая электродинамика

Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 14

Выражение (2.108) также можно записать в виде

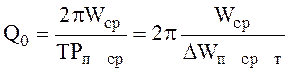,                                                              (2.109)

где  - суммарная запасенная энергия,  DWп ср т - энергия потерь за период колебаний.

Таким образом, под добротностью изолированного объема понимают увеличенное в 2p раз отношение энергии, запасенной в объеме, к потерям энергии за период колебаний. С технической точки зрения добротность определяет число периодов, за которое напряженность поля убывает в ep » 23 раза.

ГЛАВА 3

ЗАДАЧИ ЭЛЕКТРОДИНАМИКИ. ОСНОВНЫЕ ТЕОРЕМЫ И ПРИНЦИПЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ИХ РЕШЕНИЯ.

Возможны различные методы решения уравнений электромагнитного поля. При любом решении во всех случаях необходимо доказать, что решение единственно, если оно удовлетворяет уравнениям и соответствует начальным и граничным условиям. В случае неограниченного пространства вместо граничных условий решение должно удовлетворять так называемым условиям излучения. На вопрос о том, какие должны быть граничные условия, чтобы решение задачи было единственным, отвечает теорема единственности.

Существуют две основные задачи электродинамики: внутренняя и внешняя. Внутренняя задача электродинамики состоит в нахождении электромагнитного поля внутри объема V, ограниченного замкнутой поверхностью S. Внешняя задача электродинамики состоит в нахождении электромагнитного поля во всем пространстве за пределами объема V, ограниченного замкнутой поверхностью S.

Доказательство теоремы единственности рассматривают отдельно для внутренней и внешней задач электродинамики.

3.1. Теорема единственности для внутренней задачи электродинамики

Внутренняя задача электродинамики имеет единственное решение, если на границе S рассматриваемого объема V (рис. 3.1.) выполняется одно из следующих условий:

-  на всей поверхности S заданы тангенциальные составляющие вектора Е (Е - задача);

-  на всей поверхности S заданы тангенциальные составляющие вектора Н (Н - задача);

-  на одной части поверхности S1 заданы тангенциальные составляющие вектора Е, а на оставшейся части поверхности S - S1 тангенциальные составляющие вектора Н (смешанная задача). Кроме того, в объеме V имеет место хотя бы малое затухание, что в реальных условиях всегда выполняется.

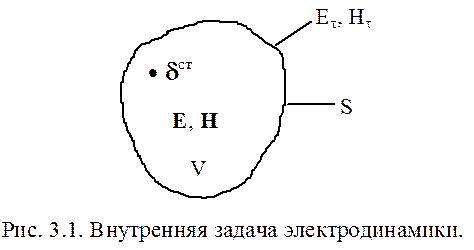
Доказательство. Предположим, что существуют два различных решения задачи. Первое решение Е1, Н1, второе решение - Е2, Н2. В силу линейности уравнений Максвелла линейная комбинация этих решений также будет решением уравнений

E3 = E1 - E2 ; H3 = H1 - H2                                                           (3.1)

Для случая монохроматического поля можно рассматривать соответствующие комплексные векторные амплитуды

                                                      (3.2)

Разностному решению соответствует система уравнений

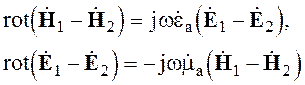                                            (3.3)

Кроме того разностное решение должно удовлетворять на поверхности S нулевым граничным условиям:

- в случае Е - задачи 

- в случае Н - задачи 

- в случае смешанной задачи 

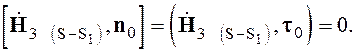
Уравнение баланса для средних значений мощности для разностного решения имеет вид

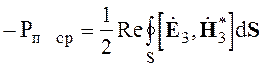                                                                     (3.4)

Если тангенциальные составляющие вектора  на поверхности S равны нулю, вектор  на поверхности S можно записать в виде

на всей поверхности S в случае Е - задачи, аналогично

 

в случае Н - задачи, на всей поверхности S. Наконец

на S и  на S - S1 .

Произведение  под знаком интеграла в любом из трех случаев будет равно нулю. Возьмем, например, первый случай Е - задачи

                               (3.5)

Здесь использовано свойство циклической перестановки множителей в смешанном произведении трех векторов. Из выражения (3.4) получаем

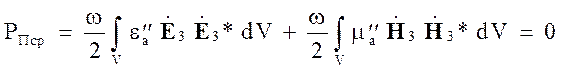                         (3.6)

По условиям теоремы затухания , следовательно,

, или , то есть

Второе решение равно первому и задача имеет единственное решение.

3.2. Теорема единственности для внешней задачи электродинамики

Скачать файл