Для
перехода от комплексных амплитуд ![]() к действительным
векторам электромагнитного поля, требуется умножить комплексные амплитуды на
временной множитель и выделить из полученного произведения действительную
часть, используя формулу Эйлера
к действительным
векторам электромагнитного поля, требуется умножить комплексные амплитуды на
временной множитель и выделить из полученного произведения действительную
часть, используя формулу Эйлера
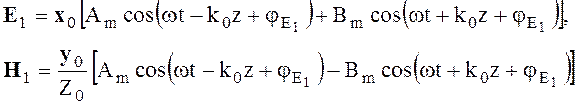 (4.33)
(4.33)
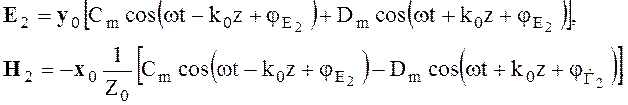 (4.34)
(4.34)
На основании выражений (4.33) и (4.34) можно сделать следующие выводы. Уравнения дают два независимых решения, каждое из которых описывает две волны. Одна из волн распространяется в положительном направлении оси z, другая - в отрицательном. Векторы электромагнитного поля Е и Н каждой из волн взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения волны. Продольные составляющие векторов Ez и Hz отсутствуют. Характеристическое сопротивление
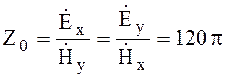 [Ом] (4.35)
[Ом] (4.35)
величина действительная, то есть векторы Е и Н находятся в фазе.
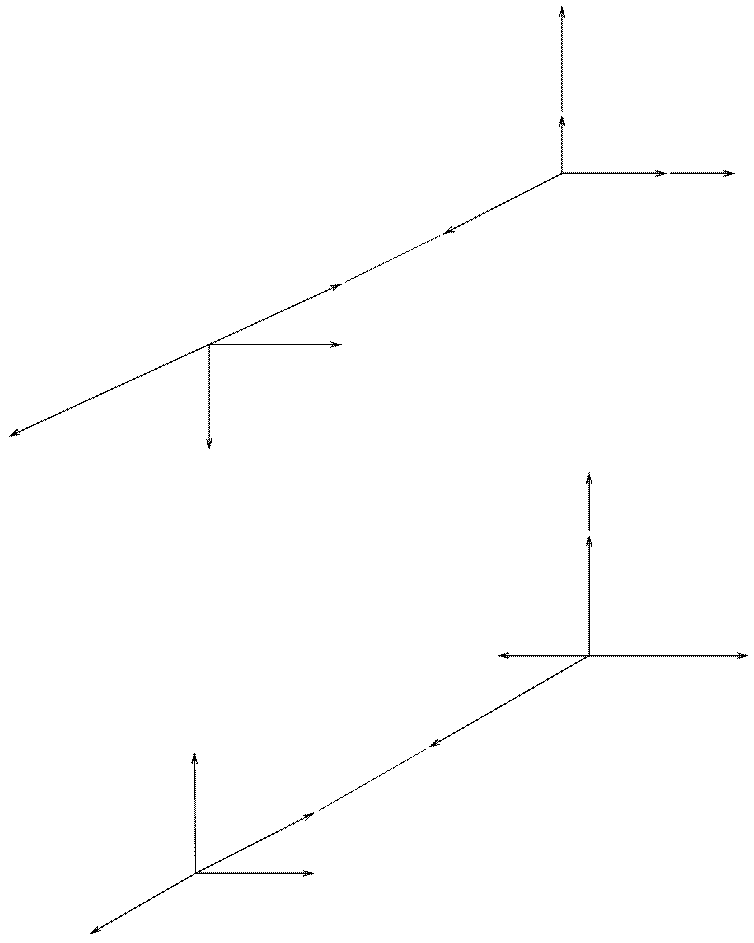
На рис. 4.1. показана взаимная ориентация векторов Е, Н и П = [Е, Н] для всех четырех волн, распространяющихся в положительном и отрицательном направлениях оси z.
На рис.4.2. показана мгновенная картина распределения значений поля при t = t1 для волны в свободном пространстве.
4.3. Волны в диэлектрике
Свойства волн в диэлектрике можно рассмотреть на примере одной волны, распространяющейся в положительном направлении оси Oz. Такая волна называется прямой. Обратные волны, распространяющиеся в отрицательном направлении оси Oz рассматриваются при изучении законов отражения и преломления электромагнитных волн.
Для диэлектрика 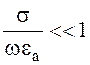 и поэтому
и поэтому 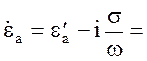
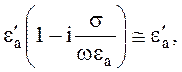 магнитная проницаемость m0.
магнитная проницаемость m0.
 y
y
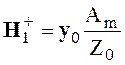
![]()
x
![]()
![]()
![]()
z 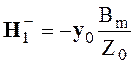 y
y
![]()
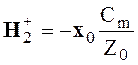 x
x
![]()
![]()
![]()
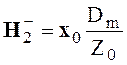
z
Рис. 4.1. Взаимная ориентация векторов четырех волн, располагающихся в
положительном и отрицательном направлениях оси Oz.
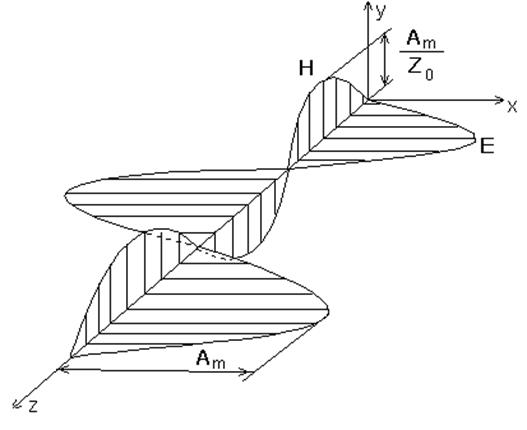
Рис. 4.2. Картина распределения значений векторов поля при t = t1 для электромагнитной волны в свободном пространстве.
Определим ![]() и
и ![]() .
.
![]() (4.36)
(4.36)
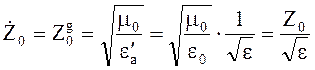 (4.37)
(4.37)
где ![]() - характеристическое сопротивление
диэлектрика.
- характеристическое сопротивление
диэлектрика.
Из выражения (4.24) имеем
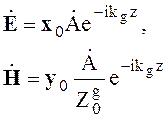 (4.38)
(4.38)
Умножая выражение (4.38) на eiwt и выделяя действительную часть получим
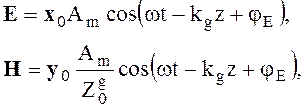 (4.39)
(4.39)
где kg
и ![]() - действительные величины.
- действительные величины.
Следовательно, векторы E и Н находятся в фазе и отношение их амплитуд равно
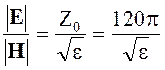 (4.40)
(4.40)
где e - относительная диэлектрическая проницаемость среды.
Определим параметры волны.
Вектор Пойтинга
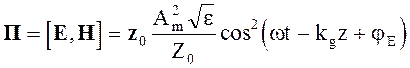 (4.41)
(4.41)
Среднее значение вектора Пойтинга
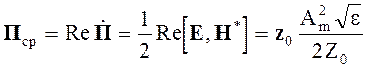 (4.42)
(4.42)
Фазовая скорость
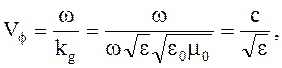 (4.43)
(4.43)
где с - скорость электромагнитной волны в свободном пространстве (скорость света).
Электрическая энергия
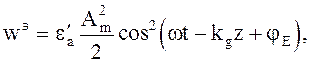
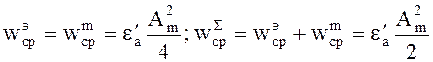 (4.44)
(4.44)
Скорость переноса энергии
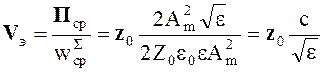 (4.45)
(4.45)
4.4. Волны в полупроводнике
В
случае полупроводника 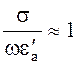 и
и ![]() -
комплексная величина. Параметры среды:
-
комплексная величина. Параметры среды: 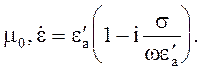
![]() (4.46)
(4.46)
где b - фазовая постоянная, a - коэффициент затухания.
Возводя в квадрат обе части уравнения (4.46) и разделяя действительную и мнимую части полученного при этом выражения, получаем для распространяющейся в положительном направлении оси Oz волны, затухающей по амплитуде
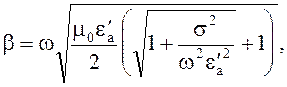 (4.47)
(4.47)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.