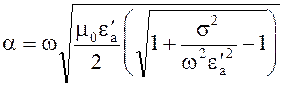 (4.48)
(4.48)
Выражения для комплексных амплитуд электрического и магнитных векторов поля принимают вид
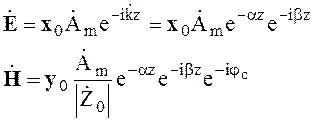 (4.49)
(4.49)
где 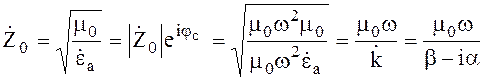 (4.50)
(4.50)
Запишем ![]() в показательном виде
в показательном виде
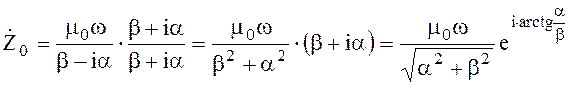 (4.51)
(4.51)
Здесь 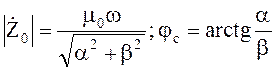 (4.52)
(4.52)
Для
получения действительных значений векторов электромагнитного поля Е и Н
умножаем комплексные амплитуды векторов на временной множитель ![]() и выделяем действительную часть полученных
выражений
и выделяем действительную часть полученных
выражений
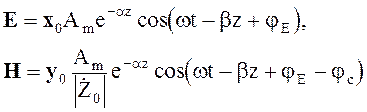 (4.53)
(4.53)
Среднее значение вектора Пойтинга
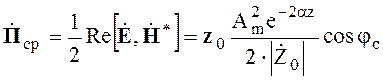 (4.54)
(4.54)
Фазовая скорость
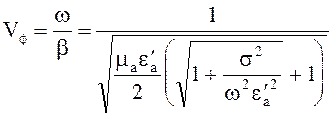 (4.55)
(4.55)
Выражение (4.55) показывает, что фазовая скорость волны в полупроводнике зависит от частоты. Зависимость фазовой скорости от частоты называется дисперсией фазовой скорости.
Электрическая энергия
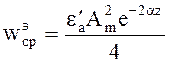 (4.56)
(4.56)
Магнитная энергия
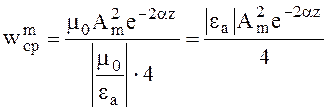 (4.57)
(4.57)
Суммарная энергия
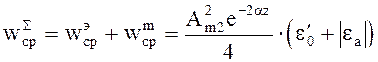 (4.58)
(4.58)
Из выражений
(4.37), (4.38) видно, что ![]() .
.
Скорость переноса энергии
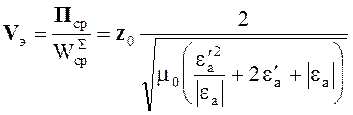 (4.59)
(4.59)
Скорость переноса энергии также зависит от частоты.
Дисперсия приводит к нежелательным явлениям при передаче информации. Передача информации в виде сигнала предусматривает модуляцию волны. При модуляции монохроматической волны образуется уже волна с несинусоидальным законом изменения векторов поля во времени. Такую волну можно разложить в спектр монохроматических составляющих (гармоник) с различными частотами. Передача информации и заключается в передаче спектра гармоник с минимальным искажением соотношений амплитуд и разности фаз между ними. Для описания скорости передачи информации применяется понятие групповой скорости.
4.5. Групповая скорость
В зависимости от вида модуляции и требований к качеству передачи информации спектр сигнала ограничивается полосой частот от w0 + Dw до w0 - Dw, где w0 - частота несущей (немодулированной) монохроматической волны. Если полоса частот 2Dw значительно меньше w0, то сумму гармоник в полосе частот называют группой волн, а скорость передачи группы волн - групповой скоростью.
Напряженность
вектора электрического поля E(t) при известном его спектре ![]() можно представить в виде
можно представить в виде
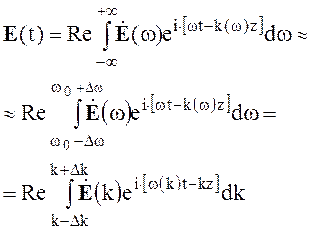 (4.60)
(4.60)
Зависимость w(k) можно представить в виде ряда Тейлора, осуществляя разложение в точке k0 по малому параметру (k - k0).
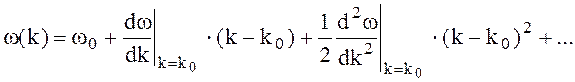 (4.61)
(4.61)
Ограничимся двумя членами разложения
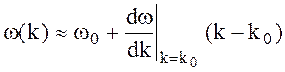 (4.62)
(4.62)
С учетом (4.62) выражение (4.60) принимает вид
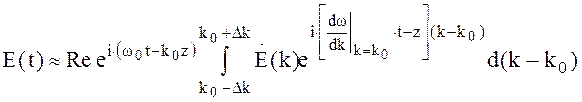 (4.63)
(4.63)
Простейший
случай ![]() в полосе значений k0 ± Dk
и множитель
в полосе значений k0 ± Dk
и множитель ![]() можно вынести за знак интеграла
можно вынести за знак интеграла
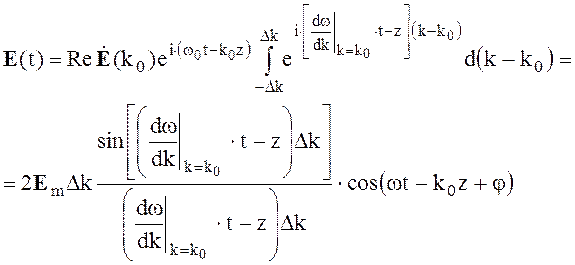 (4.64)
(4.64)
На рис.4.3. показана форма сигнала в фиксированный момент времени t=t1. Можно сделать вывод о том, что поле группы волн с одинаковыми амплитудами и фазами в интервале k0 ± Dk имеет характер модулированной монохроматической волны с огибающей, изменяющейся по закону
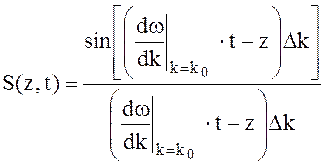 (4.65)
(4.65)
Фазовая скорость волны - это скорость движения “несущей косинусоиды” вдоль оси z
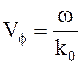 (4.66)
(4.66)
Максимум огибающей имеет место при
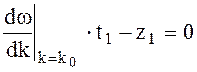
в момент времени t1
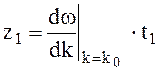
В момент времени t2 положение максимума смещается
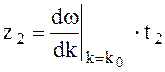
то есть
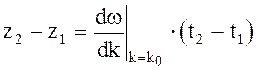
отсюда получаем
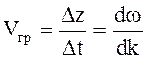 (4.67)
(4.67)
Связь между групповой и фазовой скоростью
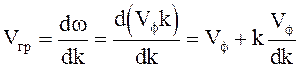 , или
, или 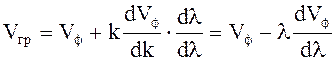 (4.68)
(4.68)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.