Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 24

                                                    (4.112)

Подставляя значение  из (4.112) в (4.106) и сравнивая с (4.112) имеем

                                                     (4.113)

Характеристическое сопротивление

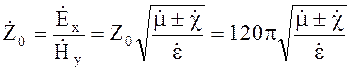                                (4.114)

Из выражений (4.112) и (4.113) видно, что векторы  и  взаимно перпендикулярны также, как и . По модулю  , а разность фаз между ними составляет ± 90⁰. Эти три условия всегда указывают на наличие круговой поляризации волны.

Комплексные амплитуды волны с правой поляризацией

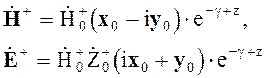                                    (4.115)

где  ; ; .

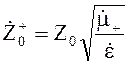Фазовая скорость волны

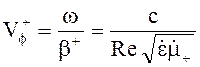                                               (4.116)

Комплексные амплитуды волны с левой поляризацией

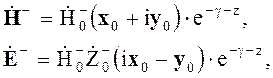                                   (4.117)

где ; ; ; .

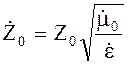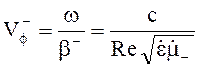Эффект Фарадея

Рассмотрим распространение плоской однородной линейно поляризованной волны в направлении оси z в гиротропной среде без потерь .

Положим, что при z = 0 линейно поляризованная волна имеет вектор  направленный вдоль оси x. Волну с линейной поляризацией всегда можно представить как две волны с круговой поляризацией правого и левого вращения с одинаковыми значениями амплитуд

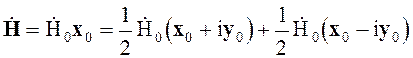                               (4.118)

при z = 0.

При дальнейшем распространении в гиротропной среде эти волны имеют разные фазовые скорости и фазовые постоянные

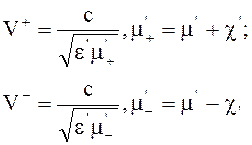                                                (4.119)

Введем среднее значение фазовой постоянной

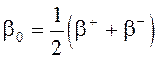                                                     (4.120)

Из выражений (4.119) и (4.120) видно, что

b⁺ = b₀ - R; b^- = b₀ + R, где 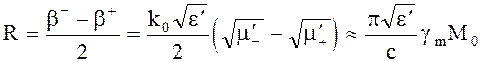                                  (4.121)

Величина R называется постоянной Фарадея.

Гиромагнитное отношение g_м связывает частоту ферромагнитного резонанса с величиной постоянного подмагничивающего поля Н₀.

f_р = g_м H₀ ,                                                     (4.122)

где g_м = 35,18  кГц  м / А.

Вектор намагниченности М₀ связан с величиной внутреннего постоянного подмагничивающего поля выражением

B = m₀ H₀ + M₀

и определяется маркой материала. Обычно при больших значениях Н₀ вектор М₀ равен по величине намагниченности насыщения.

При произвольном значении z выражение (4.118) принимает вид

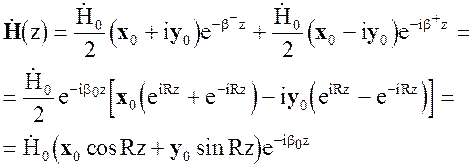                    (4.123)

Из последнего выражения видно, что вектор Н по мере распространения волны вдоль оси z поворачивается на угол

q = Rz

При распространении волны в обратном направлении направление поворота вектора относительно положительного направления оси z не меняется. Следовательно, при отражении прямой волны и возвращение в начало координат (z=0) угол q удваивается.

Явление вращения плоскости поляризации при распространении волны в гиротропных средах называется эффектом Фарадея.

Распространение плоской однородной волны вдоль оси x.

Случай поперечной намагниченности феррита

В системе уравнений (4.103) положим

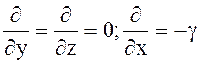                                              (4.124)

что приведет к следующим соотношениям

,

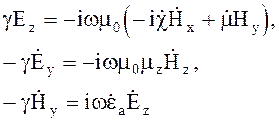                                            (4.125)

Система уравнений (4.125) распадается на две группы независимых уравнений, каждая из которых описывает отдельную волну. Одна из волн имеет две составляющие , другая волна имеет три составляющих . Первая волна называется обыкновенной волной, вторая - необыкновенной.

Обыкновенная волна

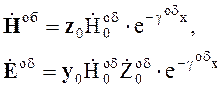                                           (4.126)

где     .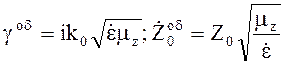

Обыкновенная волна по своим свойствам не отличается от плоской однородной среды, распространяющейся в среде с параметрами  m_a = m₀m_z   и .

В необыкновенной волне согласно (4.125)

поэтому

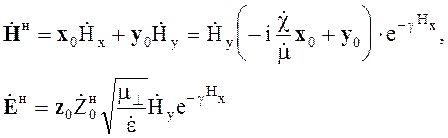                         (4.127)

где     .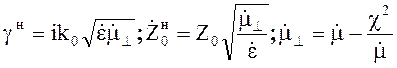

Здесь  - эквивалентная относительная магнитная проницаемость для необыкновенной волны.

На рис. 4.5. показаны векторы поля обыкновенной и необыкновенной волн.

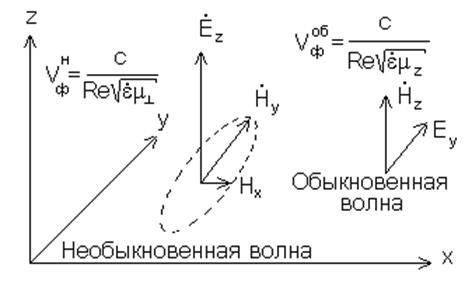
Рис. 4.5. Ориентация векторов поля в обыкновенной и необыкновенной волнах.

ГЛАВА 5

ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ЭЛЕКТРОМАГНИТЬНЫХ ВОЛН

Решение многих практических задач связано с отысканием электромагнитного поля в двух средах, разделенных границей раздела. Попадая на границу раздела электромагнитная волна может частично или полностью от нее отражаться, частично или полностью перейти в другую среду. При падении электромагнитной волны на тела ограниченных размеров, сравнимых с длиной волны, или на границу раздела сложной формы рассматривается явление дифракции электромагнитных волн.