Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 8

,                               (2.20)

запишем (2.19) в показательном виде

                                 (2.21)

Величина

,                                                         (2.22)

которая учитывает амплитуду и начальную фазу, называется комплексной векторной амплитудой.

При таком представлении процесса

                                               (2.23)

Решая уравнение электромагнитного поля для комплексных величин векторов, а затем выделяя действительную часть в полученном решении, имеем решение уравнений в виде обычных гармонических функций.

Применение метода комплексных амплитуд значительно упрощает решение системы уравнений электромагнитного поля.

Запишем систему уравнений в комплексной форме

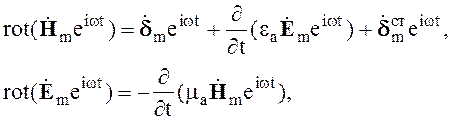
                                     (2.24)

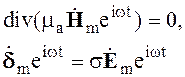
Дифференцируя по переменной t и сокращая в правой и левой частях уравнений временной множитель , получим систему уравнений для комплексных векторных амплитуд

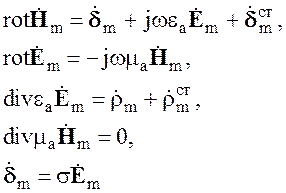                                          (2.25)

Сумму токов проводимости и токов электрического смещения в первом уравнении (2.25) можно записать в виде

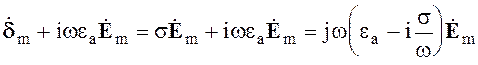                    (2.26)

Комплексной диэлектрической проницаемостью называется значение

,                                                                 (2.27)

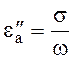где  - действительная часть комплексной диэлектрической проницаемости,  - мнимая часть комплексной диэлектрической проницаемости.

Отношение мнимой части к действительной в выражении (2.27) называется тангенсом угла диэлектрических потерь

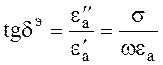                                                               (2.28)

Значения  и tgd^э приводятся в справочниках.

Магнитные потери учитываются посредством введения комплексной магнитной проницаемости

                                                          (2.29)

и тангенса угла магнитных потерь

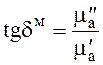                                                               (2.30)

Значения    приводятся в справочниках.

После введения понятий комплексных диэлектрической и магнитной проницаемостей система уравнений (2.25) принимает вид

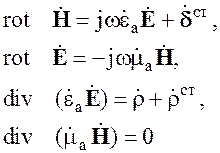                                                     (2.31)

Уравнения (2.31) записаны для комплексных векторных амплитуд. Значок “m” обычно не пишут.

Уравнение непрерывности для комплексных векторных амплитуд принимает вид

                                          (2.32)

2.2. Классификация сред

Электромагнитное поле воздействует на среду и, в свою очередь, среда воздействует на электромагнитное поле. Характер взаимодействия между электромагнитным полем и средой зависит от свойств среды.

В зависимости от значения относительной диэлектрической проницаемости все вещества можно разделить на две группы с e > 0 и e < 0. К первой группе относятся все вещества. Ко второй - плазма, представляющая собой вещества в виде сильно ионизированного газа.

В зависимости от значения относительной магнитной проницаемости все вещества подразделяются на три группы: диамагнетики (m<1), парамагнетики (m>1), ферромагнетики (m>>1).

Вводится в зависимости от отношения величин токов проводимости к величине токов смещения подразделение сред на диэлектрики, полупроводники и проводники.

Отношение величин токов проводимости и смещения определяется выражением

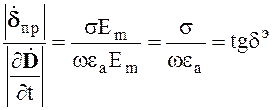                                             (2.33)

Диэлектрики (tgd^э << 1), полупроводники (tg d^э » 1), проводники (tgd^э >> 1). Из выражения (2.33) видно, что свойства среды в значительной степени зависят от частоты.

Среды подразделяются на однородные и неоднородные. Однородные среды такие, у которых параметры не являются функциями координат. Неоднородные такие, параметры которых являются функциями координат.

В зависимости от ориентации векторов Н, D и d по отношению к векторам В и Е среды подразделяются на изотропные и анизотропные. В изотропной среде вектор Н параллелен вектору В, а векторы В и параллельны вектору Е. Параметры такой среды не зависят от ориентации векторов поля в пространстве. Анизотропной называют среду, параметры которой зависят от ориентации векторов поля. Для анизотропной среды значения хотя бы одного параметра требуется записать в виде матрицы