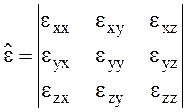(2.34)
Выражение (2.34) показывает, что каждая составляющая вектора D зависит от всех трех составляющих по координатам вектора Е
D = (exx Ex + exy Ey + exz Ez) x0 + (eyx Ex + eyy Ey + eyz Ez) y0 +
+ (ezx Ex + ezy Ey + ezz Ez) z0 (2.35)
Среды подразделяются на линейные и нелинейные. Параметры линейной среды не зависят от абсолютных значений векторов поля. Параметры нелинейной среды являются функцией абсолютного значения хотя бы одного вектора поля.
2.3. Граничные условия
Граничными условиями называются соотношения между векторами электромагнитного поля, находящимися по разные стороны границы раздела сред с различными параметрами. Под границей раздела понимают поверхность, которая разделяет две среды с различными параметрами.
Решение задач электродинамики невозможно без граничных условий. Для нахождения граничных условий используются уравнения электромагнитного поля в интегральном виде.
Граничные условия для векторов электрических составляющих
электромагнитного поля
Отдельно получим граничные условия для нормальных и тангенциальных составляющих векторов D и Е.
На рис.2.1. показана граница раздела среды 1 с параметрами ea1 и m0 среды 2 с параметрами ea2 и m0 . Значения векторов поля в среде 1 - D1, Е1, в среде 2 - D2, Е2. Выделим объем, ограниченный дифференциально малым цилиндром, одна часть которого находится в среде 1, а другая в среде 2, как показано на рисунке 2.1.
Поверхность S,
ограничивающая объем состоит из верхнего и нижнего торцов DS, внешние нормали к которым 
и боковой поверхности Sбок.
Нормаль к границе раздела сред обозначим n0, высоту цилиндра Dh.
На площадке DS, выделяемой цилиндром на поверхности раздела, распределен заряд с удельной поверхностной плотностью
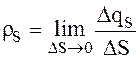(2.36)
значение которого в пределах дифференциально малой площадки DS можно считать постоянным, а саму площадку DS плоской.
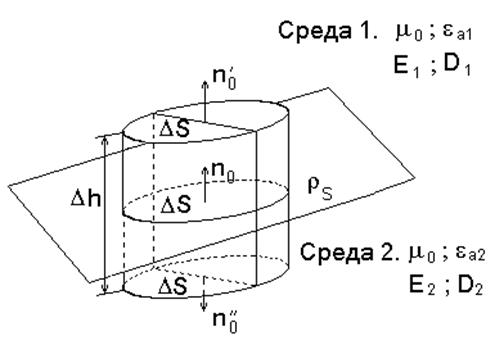
Рис 2.1. Пояснение вывода граничных условий для нормальных составляющих векторов D и Е.
Полагая, что в объеме цилиндра отсутствуют сторонние источники rст =0
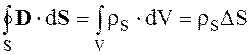(2.37)
Поток вектора D через поверхность S можно представить как сумму потоков через торцы цилиндра и боковую его поверхность
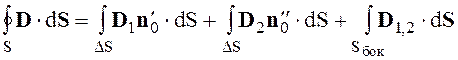
Значения векторов D1
и D2 в пределах дифференциально малых торцов цилиндра можно
считать постоянными, поэтому, вынося за знак интеграла 
,
получим
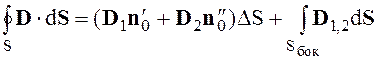(2.38)
При Dh ® 0, получаем граничные условия для нормальной Dh составляющей вектора D
D1 n0 - D2 n0 = rS (2.39)
или (D1 -D2)n0 = rS (2.40)
Нормальная составляющая вектора электрической индукции при переходе через границу раздела испытывает разрыв, равный величине удельной поверхностной плотности заряда. При отсутствии зарядов на поверхности раздела нормальные составляющие вектора D непрерывны при переходе через границу раздела
(D1 - D2)n0 = 0 или D1n = D2n (2.41)
В этом случае граничные условия для нормальной составляющей вектора Е имеют вид (при замене D1 = ea1E1 и D2 = ea2E2)
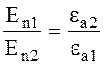(2.42)
Для вывода граничных условий для тангенциальных составляющих векторов D и Е цилиндр, изображенный на рис.2.1, рассекается по диаметру вертикальной произвольно ориентированной плоскостью и на рис.2.2. рассматривается сечение цилиндра DlDh, ограниченное контуром АВСD, при этом, кроме нормали к поверхности раздела n0 , вводится m0 - нормаль к поверхности, ограниченной контуром АВСD и t0 - касательная к поверхности раздела.
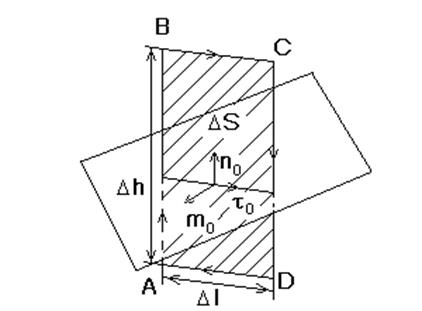
Рис 2.2. Пояснение вывода граничных условий для тангенциальных
составляющих векторов D и E.
Граничные условия для тангенциальных (параллельных поверхности раздела) составляющих векторов D и Е получаются из уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.