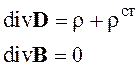 - закон Гаусса, (2.12)
- закон Гаусса, (2.12)
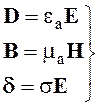 - материальные
уравнения
- материальные
уравнения
Выражения (2.12) представляют собой систему уравнений электромагнитного поля в дифференциальном виде.
Используя теоремы Стокса и Остроградского-Гаусса, можно получить систему уравнений в интегральном виде
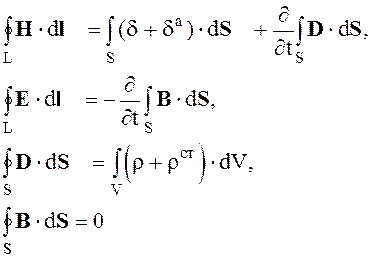 (2.13)
(2.13)
В закон Ампера Максвелл ввел член и назвал описываемый этим членом ток током смещения. Введение тока смещения позволило все ранее известные законы, описывающие электрические и магнитные явления, объединить в единую систему уравнений.
Если токи проводимости и сторонние токи обусловлены наличием проводимости среды, как видно из выражения, описывающего закон Джоуля-Ленца, то ток электрического смещения имеет две составляющие
![]()
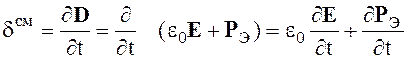 (2.14)
(2.14)
Первая составляющая - ток смещения в вакууме, вторая - поляризационный ток, образованный смещением зарядов, связанных с молекулами вещества, под воздействием электрической составляющей поля, то есть поляризацией вещества.
Ток смещения в вакууме образуется только в случае изменения электрической составляющей поля во времени. Так как никаких носителей зарядов в вакууме не существует, можно сделать вывод о том, что электромагнитное поле для своего существования не требует никакой среды, то есть оно материально.
Всякое изменение во времени электрической составляющей, согласно закону Ампера, приводит к появлению магнитной составляющей магнитного поля. В свою очередь, в соответствие с законом Фарадея, всякое изменение магнитной составляющей приводит к появлению электрической составляющей электромагнитного поля.
В соответствии с законом Гаусса возможно образование электромагнитного поля при наличии изменяющихся во времени электрических зарядов.
Так как div В = 0, можно сделать вывод об отсутствии в природе магнитных зарядов и замкнутости векторных линий магнитной составляющей поля.
Уравнения электромагнитного поля в интегральной форме удобны с точки зрения наглядности физического описания электромагнитных процессов. Для решения практических задач используются уравнения электромагнитного поля в дифференциальной форме.
Применяя операцию дивергенции к обеим частям уравнения Ампера, получим уравнение, называемое уравнением непрерывности.
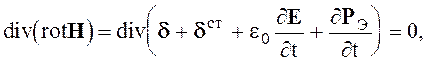 (2.15)
(2.15)
так как div (rot H) = Ñ [Ñ, H] = H [Ñ, Ñ] = 0.
С учетом закона Гаусса имеем
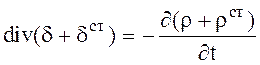 (2.16)
(2.16)
Уравнение (2.16) называется уравнением непрерывности. Оно говорит о том, что векторные линии полного тока всегда непрерывны. Следовательно, ток может протекать только в замкнутой цепи. В интегральном виде уравнение (2.16) принимает вид
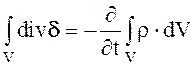 (2.17)
(2.17)
или 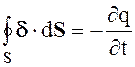 (2.18)
(2.18)
Уравнение (2.18) называется законом сохранения заряда. Закон сохранения заряда устанавливает связь между изменением заряда в объеме во времени и токами проводимости, входящими или выходящими из объема. Например, уменьшение заряда в объеме приводит к появлению токов, вытекающих из объема.
Решение системы уравнений электромагнитного поля значительно упрощается для гармонических процессов. В радиотехнике широко применяется преобразование Фурье, позволяющее представить сигнал, имеющий временную зависимость, в виде спектральной функции от частоты. Поэтому, рассматривая отдельно каждую из монохроматических составляющих спектра и решив для нее систему уравнений, можно с помощью суммирования полученных решений найти решение задачи для всего сигнала.
Монохроматические процессы записываются в виде гармонических функций косинуса или синуса.
Для упрощения решений уравнений обычно к реальной части гармонической функции косинусу добавляют мнимую часть в виде синуса и записывают таким образом монохроматический процесс в виде комплексной периодической функции
![]() (2.19)
(2.19)
Используя формулу Эйлера
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.