Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 31

Обычно не решают векторные уравнения (6.14), а определяют только продольные составляющие  и , а затем, с помощью формул, полученных из уравнений Максвелла находят поперечные составляющие.

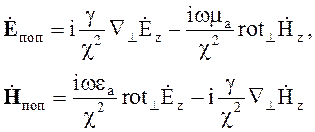                                      (6.15)

Символ ^ употребляется в качестве знака отбрасывания производных по z.

Выражения (6.15) справедливы для любой ортогональной системы координат.

ТИПЫ ВОЛН

Волна, переносящая энергию в направлении оси z, обязательно должна иметь поперечные электрическую и магнитную составляющие. При отсутствии любой из них составляющая вектора Пойтинга  будет равна нулю что говорит об отсутствии переноса энергии вдоль оси z. Поэтому волны классифицируют по наличию продольных составляющих поля.

Е - волны имеют продольную составляющую вектора  и не имеют продольной составляющей вектора .

Н - волны имеют продольную составляющую вектора Н и не  имеют продольной составляющей вектора Е.

ТЕМ - волны не имеют продольных составляющих векторов Е и Н.

НЕ - волны имеют продольные составляющие как вектора Н так и вектора Е, но по структуре поля подобны Н-волнам.

ЕН - волны имеют продольные составляющие как вектора Е так и  вектора Н, но по структуре ближе к Е-волнам.

БЫСТРЫЕ И МЕДЛЕННЫЕ ВОЛНЫ

Постоянная распространения

                                              (6.16)

Если не учитывать затухание (a = 0), то постоянная распространения g величина вещественная. При c² > 0 фазовая скорость волн будет больше скорости ТЕМ - волны в данной среде 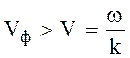. При c² < 0, то есть при мнимых поперечных волновых числах c, волны будут медленными  V_ф < V. Соотношение (6.16) удобно записать в виде

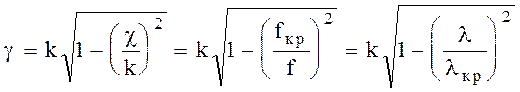,            (6.17)

где f - частота, 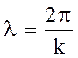- длина ТЕМ-волны в данной среде, 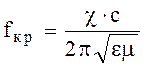 - критическая частота,  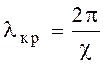- критическая длина волны.

При понижении частоты f (увеличении рабочей длины волны l) постоянная распространения g, проходя через ноль, становится чисто мнимой величиной. Поле при этом теряет свой волновой характер и не переносит энергии, а экспоненциально затухает.

Для быстрой волны, существующей при f > f_кр длина волны в структуре

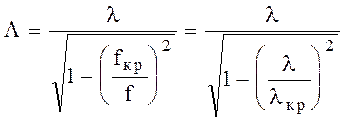                                 (6.18)

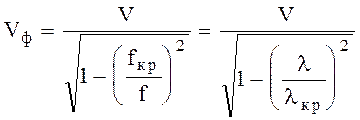                                        (6.19)

Групповая скорость

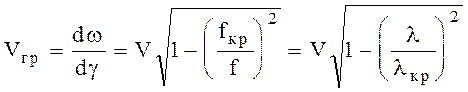            (6.20)

Быстрые волны существуют в полых металлических волноводах.

6.2. Электромагнитные волны в периодических структурах

В основном применяются продольно-периодические структуры, показанные на рис. 6.2.

Электромагнитные поля в продольно-периодических структурах подчиняются теореме Флоке, которая выражает следующее свойство комплексных амплитуд

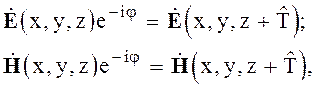                                     (6.21)

где j - вещественная величина, если отсутствует поглощение.

Из (6.21) следует, что при сдвиге на величину пространственного периода структуры  наблюдается фазовый сдвиг j без каких-либо других изменений поля.

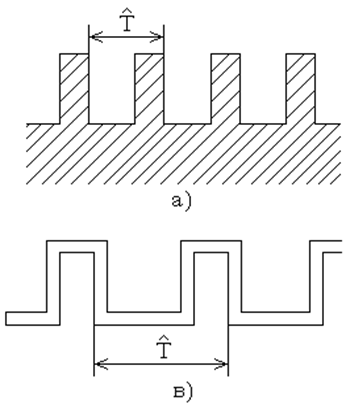
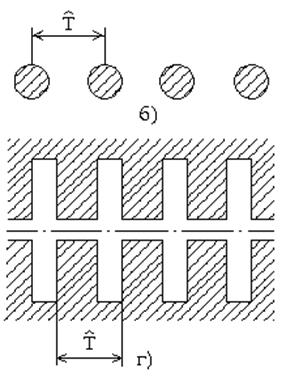
Рис. 6.2. Продольно-периодические структуры.

а) гребенчатая структура, б) система поперечных стержней, в) проволочная периодическая структура, г) ребристый волновод

Исходя из (6.21), можно записать периодические по z функции, введя параметр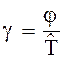

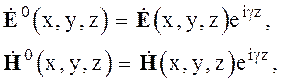                                 (6.22)

где 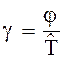 - специально введенный параметр.

Множитель  компенсирует фазовый сдвиг, возникающий согласно (6.21) на отрезке структуры длиной .

Разложим функцию  по пространственным гармоникам

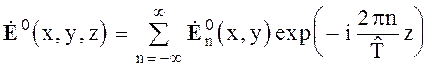,                 (6.23)

где 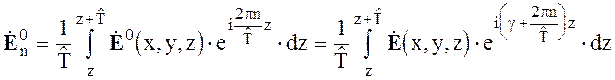          (6.24)

Аналогично можно записать .

Введя множитель ехр(-igz) снова перейдем от  и  к  и

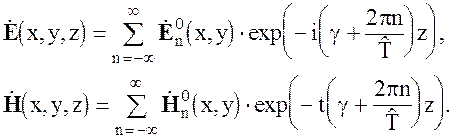                         (6.25)

На основании (6.25) можно сделать заключение, что всякий волновой процесс в периодической структуре, создающей фазовое запаздывание j на протяжении ее периода , эквивалентен наложению бесконечного числа плоских неоднородных волн с комплексными амплитудами ,  и постоянной распространения

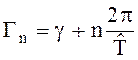  (n = 0, ±1, ±2, ... , ±¥)                             (6.26)

Эти волны, называемые пространственными гармониками, имеют фазовые скорости

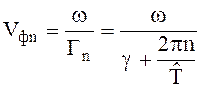                                              (6.27)

и одну общую групповую скорость

.

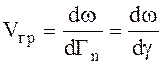Так как n = 0, ±1, ±2, ... , ±¥, то фазовая скорость пространственных гармоник может как совпадать по направлению с групповой, так и быть ей противоположной. Их называют прямыми и обратными волнами.