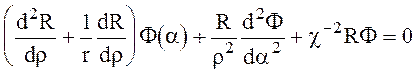Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 33

                               (6.43)

Умножим все члены (6.43) на  и получим

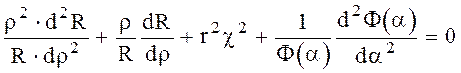                       (6.44)

Первые три члена в выражении (6.44) зависят только от r, а последний - от a.

Введем постоянную n² и приравняем к ней первые три члена

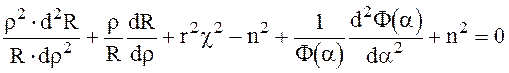               (6.45)

Из (6.45) получаем два обыкновенных дифференциальных уравнения

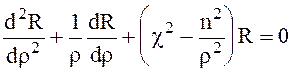,                                        (6.46)

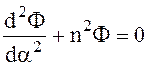.                                            (6.47)

Обыкновенное дифференциальное уравнение (6.46) - это уравнение Бесселя. Его общее решение имеет вид

R(r) = A J_n (cr) + B N_n (cr)                                   (6.48)

Решение уравнения (6.47) нам известно

F(a) = cos na + sin na

Таким образом

(r,a) = [ J_n(cr) + N_n(cr)] (cos na + sin na)             (6.49)

Функции J_n(cr) и N_n(cr) в (6.49) называются цилиндрическими функциями.

J_n(u) - функции Бесселя n-го порядка, N_n(u) - функции Неймана n-го порядка, где  u = cr. Вид функций Бесселя и Неймана показан на рис.6.5 и рис.6.6.

Отметим что J₀(0) = 1, J_n(0) = 0 при n ¹ 0 и N_n(0) = -¥. Значения аргумента u, при котором функции Бесселя и их первые производные обращаются в нуль приводятся в таблицах 6.1 и 6.2. Здесь n - порядок функции Бесселя, m - номер корня.

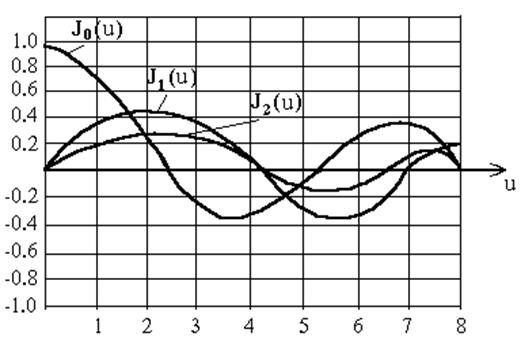
Рис. 6.5. Вид функций Бесселя.

 

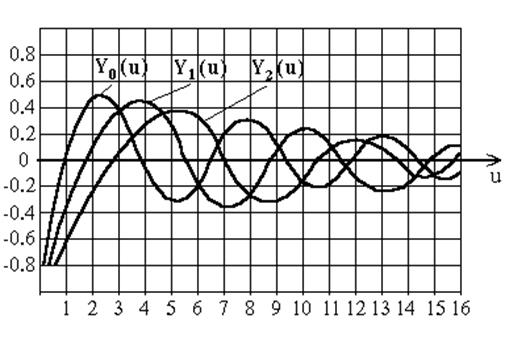
Рис. 6.6. Вид функций Неймана.

Приведем некоторые соотношения, справедливые для функций Бесселя и Неймана.

Таблица 6.1                                                         Таблица 6.2

Корни  u_nm   уравнения J_n(u) = 0                          Корни u¢_mn уравнения (u) = 0

n			m			n			m
	1	2	3	4			1	2	3	4
0	2,405	5,520	8,654	11,792		0	3,832	7,016	10,173	13,324
1	3,832	7,016	10,173	13,324		1	1,841	5,331	8,536	11,706
2	5,136	8,417	11,620	14,796		2	3,054	6,706	9,969	13,170
3	6,380	9,761	13,015	16,223		3	4,201	8,015	11,346	14,586

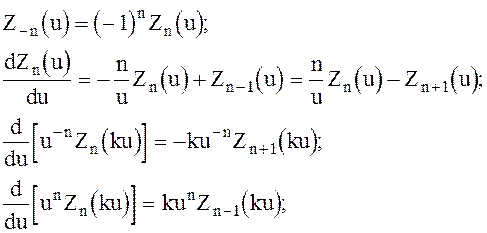
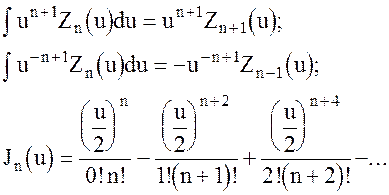                                             (6.50)

Рассмотрим решение краевых задач в случае кольцевой и круговой областей, показанных на рис. 6.7.

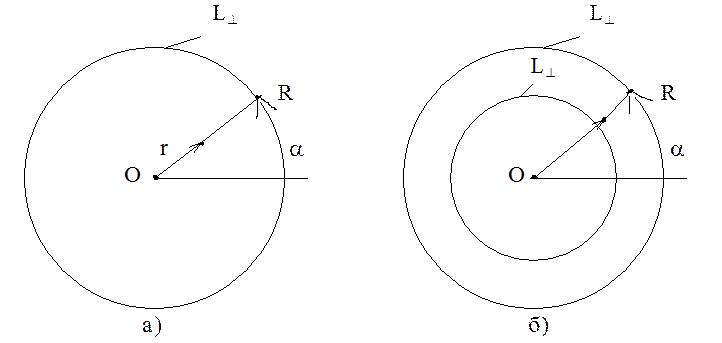
Рис. 6.7. Области, для которых решаются краевые задачи в случае цилиндрических координат

Поскольку для таких областей Т(r, a + 2pn) = T(r, a), то значение n будет целое или нуль.

Для круговой области, показанной на рис.6.7 а, при r = 0 N_n(x) стремится к бесконечности, поэтому, исходя из чисто физических соображений следует положить коэффициент В = 0 и выражение (6.49) примет вид

                             (6.51)

В случае первой краевой задачи (r, a) = 0 при r = R, откуда следует,

J_n(c R) = 0                                           (6.52)

Корни уравнения (6.52) u_nm = R приведены в таблице 6.1.

Теперь можно записать решение первой краевой задачи

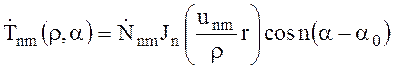,              (6.53)

где 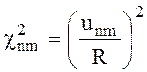                                                                                          (6.54)

Решение для круговой области второй краевой задачи при граничном условии 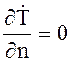 при r = R дает

                                                 (6.55)

Следовательно

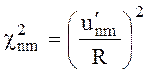                                              (6.56)

В случае кольцевой области В ¹ 0 в (6.49) и для первой краевой задачи получаем (r, a) = 0, при r = R₁; r = R₂. Отсюда

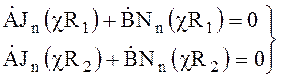                                 (6.57)

Для получения ненулевого решения определитель этой системы должен быть равен нулю

J_n(cR₁) × N_n(cR₂) - J_n(cR₂) × N_n(cR₁) = 0                          (6.58)

Это уравнение позволяет найти корни . Подставляя  в одно из уравнений (6.57), можно найти отношение коэффициентов  и . Получим

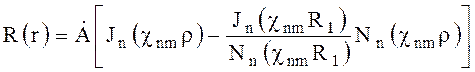                     (6.59)

Окончательно

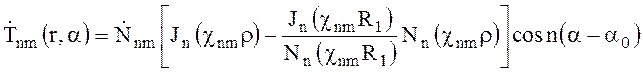          (6.60)

Для второй краевой задачи при кольцевой области 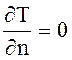 при r = R₁; r = R₂. Следовательно, имеем систему уравнений для определения