Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 26

Для получения соотношения между w^п, w^отр, w^пр запишем выражения для векторов напряженности электрического поля из (5.5) в виде произведения двух функций, одной, зависящей только от координат, другой - только от времени.

                          (5.6)

На границе раздела сред (при z = 0) выполняются граничные условия для тангенциальных составляющих напряженности электрического поля

                                                      (5.7)

или                                                                 (5.8)

так как векторы  как будет показано дальше, направлены вдоль оси х.

Дифференцируя обе части выражения (5.8) по переменной t, получаем

                             (5.9)

Подставим значение  из (5.8) в (5.9) и получим

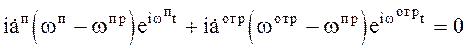
Последнее равенство должно тождественно выполняться для любых значений t, а это возможно лишь при условии w^п = w^отр.  Аналогично, заменяя в (5.9) из (5.8) , получим w^п = w^пр. Можно сделать вывод, что частота при отражении и преломлении не изменяется.

Для получения соотношений между также применим граничное условие

Запишем его в виде

                                  (5.10)

где  не зависят от положения (координат) точки на границе раздела.

Применим к обеим частям (5.10) операцию

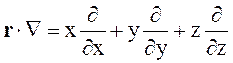
Учитывая, что , получаем

                (5.11)

исключая из правой части (5.11)  с помощью (5.10) получаем соотношение

                     (5.12)

Оно справедливо для любой точки поверхности раздела, то есть при произвольном значении r, что возможно лишь при условии

                                                           (5.13)

Если в (5.11) заменить  с помощью равенства (5.10) и провести аналогичные рассуждения, то получим соотношение

                                                           (5.14)

Таким образом

                                                 (5.15)

Вектор r лежит в плоскости раздела сред, а в остальном произволен. Выберем его в направлении, перпендикулярном одному из волновых векторов, например k^п. Тогда условие (5.15) приобретает вид

                                           (5.16)

Это означает, что векторы k^отр и k^пр также перпендикулярны вектору r, то есть лежат в той же плоскости, что и вектор k^п.

В соответствии с рис. 5.2.

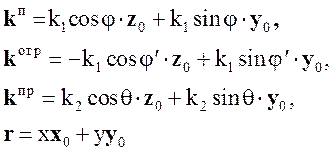                                   (5.17)

Подставляя значения k^п, k^отр, k^пр и r из (5.17) в (5.15), получаем

k₁y sin j = k₁y sin j¢ = k₂y sin q.                                      (5.18)

Здесь

Выражение (5.18) устанавливает соотношения между углами падения, отражения и преломления с учетом параметров сред k₁ и k₂.

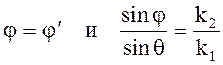
Учитывая,  что  согласно  полученным  соотношениям  w^п = w^отр = w^пр  и k^пr = k^отрr = k^прr на границе раздела, получаем граничные условия (5.7) в виде

,                                           (5.20)

так как экспоненциальные множители одинаковы. В (5.20)  - комплексные амплитуды векторов. Соотношения между ними называются формулами Френеля.

Для получения формул Френеля запишем граничные условия для тангенциальных составляющих векторов . Имеем при z = 0

или, учитывая, что для плоской однородной волны

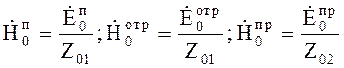
имеем 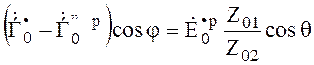         .                           ???               (5.21)

Отношение комплексных амплитуд отраженной и падающей волн называется коэффициентом отражения. Отношение комплексных амплитуд прошедшей и падающей волн - коэффициентом прохождения.

Разделим выражения (5.20) и (5.21) на  и получим систему уравнений для определения коэффициентов отражения r и прохождения t

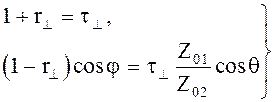                                            (5.22)

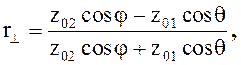                                                  (5.23)

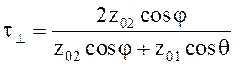                                                   (5.24)

В случае падения плоской однородной волны из воздуха (среда1) в проводящую среду (среда 2)

,

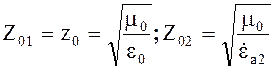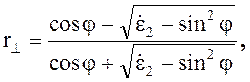
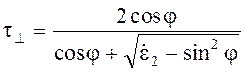                                                 (5.25)

где 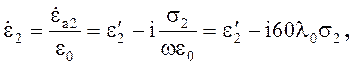  - активная оставляющая относительной комплексной диэлектрической проницаемости среды 2, l₀ - длина волны в среде 1.

Закон преломления принимает вид

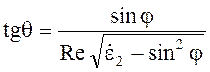                                             (5.26)

Для среды с потерями коэффициенты t_^ и r_^ зависят от частоты, угол преломления является также функцией частоты и проводимости s.