При значении ![]() на расстоянии длины волны укладывается
большое число пространственных периодов. Такая структура может быть названа
частой периодической структурой.
на расстоянии длины волны укладывается
большое число пространственных периодов. Такая структура может быть названа
частой периодической структурой.
Если структура частая, то можно считать, что по отношению к верхнему полупространству граница структуры х = 0 (рис. 6.3) проявляет некоторые усредненные свойства, а волновой процесс определяется главным образом нулевой гармоникой.
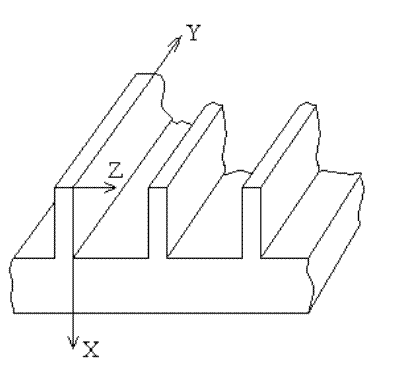
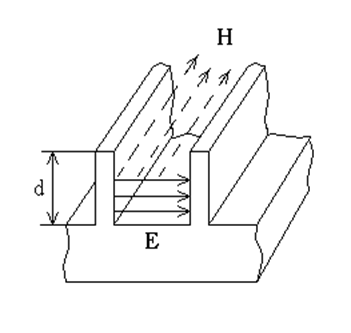
Рис. 6.3. Частая периодическая структура.
В пазах структуры может существовать поле, показанное на рис.6.3. Волновой процесс можно считать в целом Е - волной. Можно считать поле в пределах паза не изменяющимся в направлении оси z, а в направлении оси х поле образует стоячую ТЕМ - волну, в которой
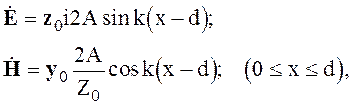 (6.28)
(6.28)
так как выполняется граничное условие ![]() при
х = d.
при
х = d.
Между комплексными амплитудами на поверхности х = 0 можно найти следующее соотношение
![]() (6.29)
(6.29)
где Z0 = 120 p - характеристика сопротивления свободного пространства.
Пренебрегая площадью ребер при х = 0, можно сказать, что эта граница структуры проявляет себя как ипедансная поверхность, характеризуемая ипедансом ZS.
Можно сделать вывод, что вдоль частой ребристой поверхности будет распространяться поверхностная Е - волна, по аналогии распространения Е - волны вдоль поверхности раздела двух сред при углах падения больших критического и параллельной поляризации падающей на поверхность раздела волны.
Фазовая скорость такой волны меньше фазовой скорости волны в свободном пространстве, то есть волна замедленная. В этом случае ребристая структура играет роль “искусственного диэлектрика”.
6.3. Решение двухмерного уравнения Гельмгольца методом разделения переменных
Двумерное уравнение Гельмгольца как было показано в 6.1 имеет вид
![]() (6.30)
(6.30)
В декартовой системе координат двумерное уравнение Гельмгольца имеет вид
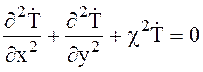 (6.31)
(6.31)
Предположим, что ![]() можно представить в виде произведения
функций разных координат
можно представить в виде произведения
функций разных координат ![]() .
.
Подставим это представление в (6.28) и получим
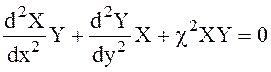
После деления всех членов на ХY имеем
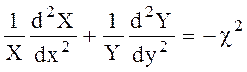 (6.32)
(6.32)
Слагаемые в уравнении
(6.32) - функции разных аргументов, то есть они независимы, а следовательно
каждое слагаемое равно постоянной величине. Обозначим эти постоянные величины
как ![]() и
и ![]() .
Очевидно, что
.
Очевидно, что ![]() .
.
Вместо (6.29) получаем два обыкновенных дифференциальных уравнения
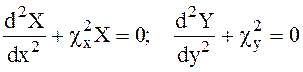 (6.33)
(6.33)
Общее решение дифференциальных уравнений, как известно, можно найти как в тригонометрической, так и в экспоненциальной форме. Выберем тригонометрическое представление
Х = ![]() соscx
x +
соscx
x + ![]() sincx
x;
sincx
x;
Y = ![]() cos cy y +
cos cy y + ![]() sin cy y; (6.34)
sin cy y; (6.34)
Для первой краевой
задачи, рассматривая прямоугольную область, показанную на рис.6.4, граничное
условие ![]() на L^ означает следующие требования
на L^ означает следующие требования
![]() при х = 0; у = 0; х = а; у = b.
при х = 0; у = 0; х = а; у = b.
![]() . (6.35)
. (6.35)
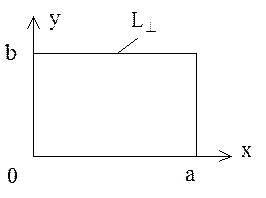
Рис. 6.4. Постановка краевых задач для прямоугольной области
с границей L^.
Из граничных условий Т(0,
у) = Т(х, 0) = 0 получаем ![]() =
= ![]() = 0. Из условий
= 0. Из условий ![]() (а,
у) =
(а,
у) = ![]() (х, в) = 0 получаем
(х, в) = 0 получаем 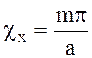 ;
;
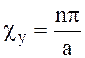 , где m, n = 1, 2, 3...
, где m, n = 1, 2, 3...
Окончательно имеем
![]() (х, у) = N sin
(х, у) = N sin ![]() x × sin
x × sin![]() y (6.36)
y (6.36)
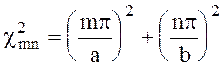 (6.37)
(6.37)
Функции
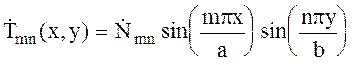 (6.38)
(6.38)
называются собственными функциями, которым соответствуют
собственные значения ![]() ,
, ![]() -
неопределенные постоянные.
-
неопределенные постоянные.
Для второй краевой задачи
на решение (6.35) следует наложить условие 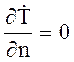 , на L^ , что означает
, на L^ , что означает
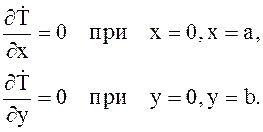 (6.39)
(6.39)
Дифференцируя выражение
(6.35) по х, а затем по у и приравнивая согласно (6.39) к нулю производные,
находим, что В = D = 0 и 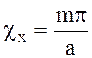 ;
; 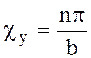 . Теперь
. Теперь
![]() (6.40)
(6.40)
Теперь собственные функции принимают вид
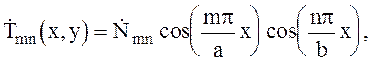 (6.41)
(6.41)
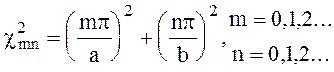
Теперь значения m = 0, n = 0 не исключатся.
В цилиндрической системе координат двумерное уравнение Гельмгольца имеет вид
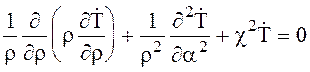 (6.42)
(6.42)
Решение уравнения ищем в
виде произведения ![]() .
.
Подставим записанное значение ![]() в (6.42) и получим
в (6.42) и получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.