Векторно-скалярное произведение можно представить в форме определителя
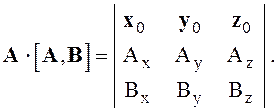(1.11)
Если определитель равен нулю, то векторы А, В и С компланарны.
Двойное векторное произведение
A ´ [B, C] = B (A, C) - C (A, B) (1.12)
В двойном векторном произведении важен порядок перемножения
A ´ [B, C] = B (A, C) - C (A, B)
B ´ [C, A] = C (B, A) - A (B, C) (1.13)
C ´ [A, B] = A (C, B) - B (C, A)
Складывая эти три равенства, получим
A ´ [B, C] + B ´ [C, A] + C ´ [A, B] = 0 (1.14)
Важное применение формулы (1.12) состоит в выводе разложения данного вектора В на две составляющие, из которых одна параллельна, а другая перпендикулярна вектору А. Положим в формуле (1.12) С = А и получим
A ´ [B, A] = B (A, A) - A (A, B) = B A2 - A (A, B)
Отсюда
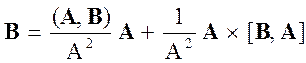(1.15)
Первый вектор параллелен А, а второй перпендикулярен А.
1.2. Поля и операции векторного анализа.
Под термином «поле» понимают часть пространства, в каждой точке которой задана скалярная или векторная величина, в зависимости от того, какая функция (скалярная или векторная) изучается. Очень часто приходится рассматривать скалярные или векторные функции, изменяющиеся с течением времени: j(r,t); a(r,t). Соответствующие поля называются тогда переменными или нестационарными. Поля, не изменяющиеся с течением времени, называют постоянными или стационарными.
Скалярное поле. Пусть задана скалярная функция j(х, у, z). Если задано нестационарное поле, то можно рассматривать его в определенный момент времени. Поле можно изобразить в виде семейства поверхностей уровня j(х,у,z)= const. На рис.1.6. показано сечение такого семейства плоскостью чертежа.
Векторное поле. Для графического представления векторного поля используются векторные линии, то есть такие линии, касательные к которым в заданных точках показывают направление вектора в рассматриваемых точках, как показано на рис.1.7.
Рис.1.6. Семейство поверхностей уровня.
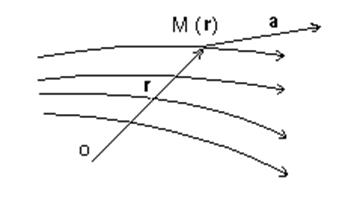
Рис. 1.7. Семейство векторных линий.
Возьмем на векторной линии точку М(r). Единичный вектор касательной к векторной линии есть dr/ds, но по условию вектор а в точке М должен касаться векторной линии, следовательно, два вектора а и dr/ds коллинеарны, поэтому
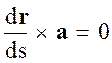(1.16)
или, умножая на ds, получаем
dr ´ a = 0 (1.17)
Это есть дифференциальное уравнение векторных линий в векторной форме.
Обозначим составляющие а(r) как aх (х, у, z), aу (х, у, z), az (х, у, z),
r = x x0 + y y0 + z z0 . Теперь d(xx0 + yy0 + zz0 ) ´ (ax x0 + ay y0 +az z0) = 0
или
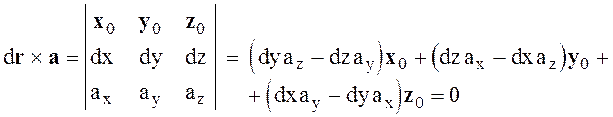(1.18)
Из (1.18), приравнивая каждую из компонент в правой части, получим уравнение векторных линий
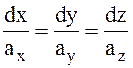(1.19)
Для определения величины
вектора можно поступить двумя способами. Имея в виду, что величина вектора есть
скаляр, следует рассмотреть векторное поле как скалярное поле модуля вектора и
построить соответствующие поверхности 
=
const.
Другой способ характеризует величину вектора густотой проводимых векторных линий. Густоту линий измеряют, проводя через рассматриваемую точку маленькую, перпендикулярную к линии площадку, отсчитывая на площадке число пересечений ее векторными линиями и относя это число к единице площади.
Свойства полей характеризуются с помощью целого ряда характеристик и параметров.
Скалярное поле, заданное функцией j(r) = j(х, у, z), можно отобразить в виде семейства уровней j(х, у, z) = const. Для его описания вводится вектор grad j.
Градиентом j называется вектор, имеющий направление быстрейшего увеличения j и по величине равной производной по этому направлению. В декартовой системе координат
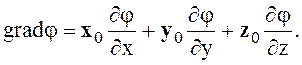(1.20)
Величина grad j равна
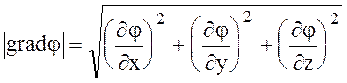(1.21)
Производная по любому направлению s0 равна проекции grad j на это направление
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.