Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 18

Из уравнений (4.12) определяются составляющие вектора . Значения составляющих вектора  определяются из уравнений Максвелла, записанных в декартовой системе координат, при условии ;  и .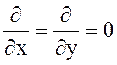

Первое уравнение

в декартовой системе координат имеет вид

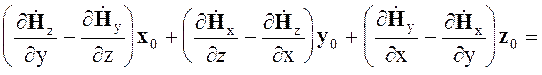
При 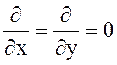 имеем

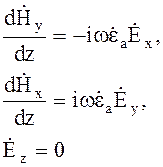                                                                               (4.13)

Из второго уравнения Максвелла можно аналогично получить

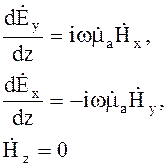                                                                              (4.14)

Выражения (4.13), (4.14) образуют две независимые системы уравнений

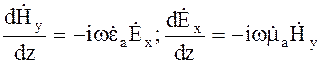                                                       (4.15)

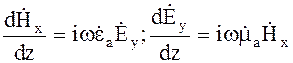                                                              (4.16)

Теперь можно сделать вывод, что для решения векторных волновых уравнений в частных производных

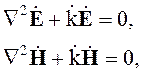
описывающих плоские однородные волны, достаточно решить два обыкновенных дифференциальных уравнения

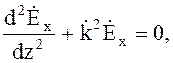                                                                             (4.17)

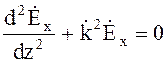                                                                              (4.18)

и затем, подставив полученные значения в уравнения (4.15), (4.16)

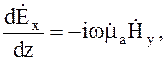                                                                              (4.19)

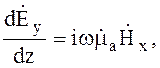                                                                                (4.20)

получить значения составляющих  и ; согласно (4.13), (4.14)  и

Решение уравнения (4.17) имеет вид

                                                                        (4.21)

Из уравнения (4.20) определяем

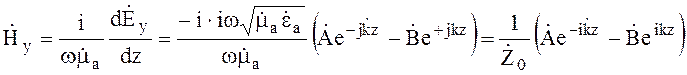               (4.22)

Решение уравнения (4.18) имеет вид

Из уравнения (4.20) определяем

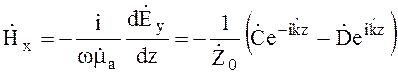                                    (4.23)

В результате получены два решения системы уравнений Максвелла для плоских однородных волн

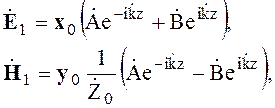                                                                  (4.24)

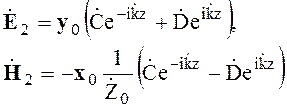                                                               (4.25)

Величина , представляющая отношение комплексных амплитуд поперечных составляющих электромагнитного поля, называется характеристическим сопротивлением среды.

Для свободного пространства

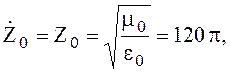                                                               (4.26)

где Z₀ - характеристическое сопротивление свободного пространства.

В общем случае в случае наличия потерь  и значение характеристического сопротивления комплексное

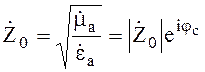                                                                     (4.27)

Рассмотрим волны дальше в различных средах: в свободном пространстве, диэлектрике, полупроводнике и проводнике.

Как видно из выражений (4.24), (4.25) для получения двух выражений, описывающих волну (4.24) или (4.25), необходимо найти два параметра:  - волновое число и  - характеристическое сопротивление, которые полностью определяются параметрами среды и частотой

                                                                                       (4.28)

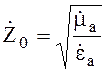                                                                                             (4.29)

При рассмотрении волн в различных средах будем записывать параметры, характеризующие среду, с помощью их находить  и , далее из уравнений (4.24), (4.25) определять значения комплексных амплитуд векторов  и электромагнитного поля. Умножая значения комплексных амплитуд на  и выделяя действительную часть полученных выражений будем получать выражения, описывающие электромагнитные волны в соответствующей среде.

4.2. Электромагнитные волны в свободном пространстве.

Под свободным пространством понимают безвоздушное пространство и близкую к нему по параметрам часть атмосферы.

Параметры свободного пространства e₀, m₀. Следовательно,

                                                                                    (4.30)

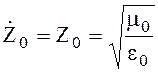                                                                                 (4.31)

Подставляя значения  [Гн/м] и 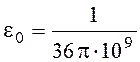 [Ф/м] получим Z₀ = 120 p [Ом].

Выражения для комплексных амплитуд векторов (4.24) и (4.25) принимают вид

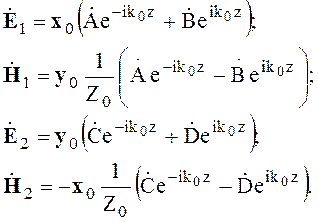                                                        (4.32)