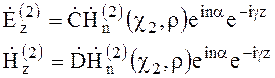Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 40

                                            (6.148)

Поперечные составляющие электрического и магнитного полей, касательные к границе раздела, определяем из соотношений (6.92)

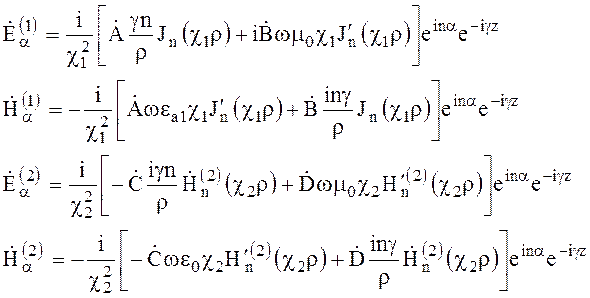  (6.149)

Для определения постоянной распространения g воспользуемся граничными условиями на внешней поверхности диэлектрического волновода, то есть при r = R.  Исходя из того, что на этой поверхности тангенциальные составляющие составляющих поля  и  должны быть непрерывны. Запишем следующие соотношения:

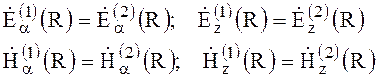                           (6.150)

Подставляя (6.147) - (6.149) в (6.150), получим следующее трансцендентное уравнение (исключая из системы неизвестные коэффициенты , , , ).

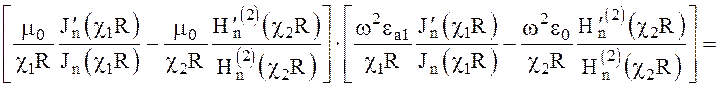
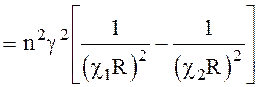                                                                             (6.151)

Это уравнение служит для определения неизвестной постоянной распространения g, которая связана с равенством

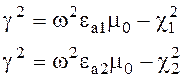                                        (6.152)

После подстановки (6.152) в (6.151) уравнение может быть решено относительно g.

Волны, распространяющиеся вдоль диэлектрического волновода, аналогичны поверхностным волнам, описываемых в разделе 5.4, где показано, что поперечное волновое число в среде 2 имеет мнимое (-ja), следовательно и k₂ в нашем случае имеет чисто мнимое значение. При значении n=0 поле по координате a не изменяется, то есть является симметричным относительно оси волновода. Уравнение (6.151) распадается на два

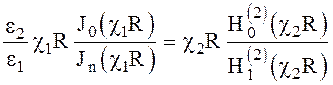 - E волны                            (6.153)

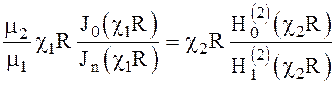 - Н волны                           (6.154)

Полученные выражения справедливы для волн Е_0m и Н_0m.

Симметричные волны редко применяются на практике. Критические длины волн для волн типа Е_0m и Н_0m одинаковы

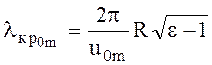,                                            (6.155)

где u_0m - корни уравнения J₀(u_0m) = 0.

Значения корней уже приводились ранее при рассмотрении круглого волновода с металлическими стенками в табл. 6.1. Критическими длинами волн для диэлектрического волновода считаются такие, при которых постоянная распространения g диэлектрического волновода соответствует постоянной распространения k₂ в среде 2. В этом случае диэлектрический волновод не оказывает никакого воздействия на волну, распространяющуюся в его присутствии.

Так как

, то такое условие выполняется при  = 0, то есть k = g.

Выражение (6.151) при  можно преобразовать к виду [1]

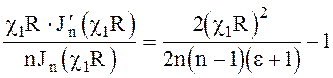  при  n > 1                          (6.156)

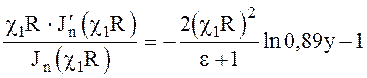                                       (6.157)

При  . Следовательно, в левой части (6.157)

                                                             (6.158)

Значения корней u_1m также приведены в таблице 6.1. Для волны НЕ₁₁ u_1m = 0.

Волны Н_nm и Е_nm могут существовать в диэлектрическом волноводе только одновременно образуя гибридные волны НЕ_nm и ЕН_nm, так как имеют одинаковые критические длины волн.

Диаграмма типов волн диэлектрического круглого волновода приведена на рис.6.24.

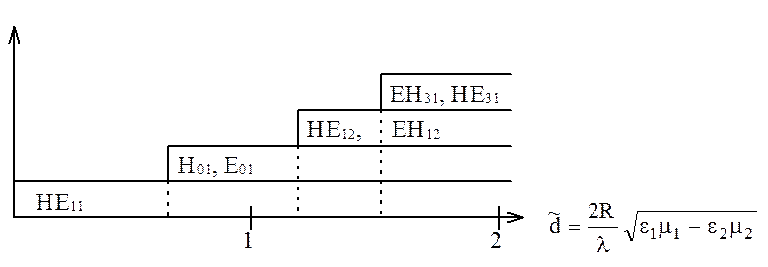
Рис. 6.24. Диаграмма типов волн диэлектрического круглого волновода. Здесь  - приведенный диаметр диэлектрического волновода.

Из диаграммы типов волн видно, что основная волна - НЕ₁₁. Она наиболее часто и используется. Рассмотрим ее параметры.

При критической длине волны фазовая скорость равна скорости света в свободном пространстве по мере уменьшения длины волны фазовая скорость уменьшается, приближаясь к величине фазовой скорости в неограниченной среде, заполненной диэлектриком с относительной диэлектрической проницаемостью

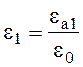
то есть к скорости

Зная  для волны НЕ₁₁, легко получить выражение для фазовой скорости

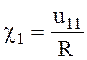
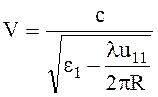                                            (6.159)

В диэлектрическом волноводе часть энергии переносится внутри стержня, другая часть в пространстве, окружающем стержень. Поэтому большое значение имеет выбор диаметра волновода, при котором большая часть энергии переносится по стержню и в ближайшей окрестности стержня.

Полная энергия, проходящая через поперечное сечение волновода, равна

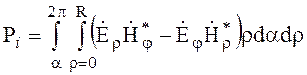                                       (6.160)

полная энергия, проходящая по внешнему пространству, равна

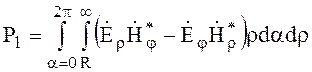                                      (6.161)

Для волны НЕ₁₁ выражения для составляющих поля в среде 1 (внутри стержня) имеют вид