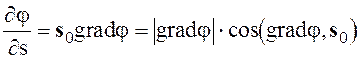(1.22)
Видно, что скалярное поле j порождает векторное поле F = grad j. Такое векторное поле называется потенциальным, а скалярная функция j - потенциалом. Поверхности уровня, являются, как говорят, эквипотенциальными поверхностями.
Векторное поле, заданное функцией F = (x, y, z) = F(r), можно описать двумя характеристиками: дивергенцией (расхождением) и ротором (вихрем).
Рассмотрим несколько разновидностей векторных полей, изображенных на рис. 1.8 в виде векторных линий
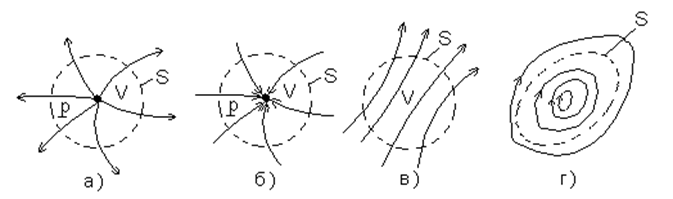
Рис. 1.8. Разновидности векторных полей.
Точка R в которую сходятся векторные линии называется стоком.
Точка R из которой расходятся векторные линии, называется истоком.
Введем понятие потока вектора F через поверхность S (не обязательно замкнутую)
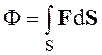,(1.23)
где dS понимается как произведение dS на орт нормали к поверхности n.
dS = n dS (1.24)
Если поверхность S замкнутая, как показано на рис. 1.8, то символ интеграла дополняется кружком
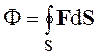(1.25)
Выходящие наружу векторные линии считаются положительными, входящие внутрь векторные линии - отрицательными. В зависимости от преобладания входящих или выходящих из объема V векторных линий поток может быть положительным (рис. 1.8,а), отрицательным (рис. 1.8,б) или равным нулю (рис.1.8, в, г).
Дивергенцией вектора F называется скалярная величина, определяемая следующим предельным соотношением
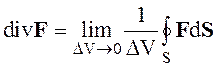, (1.26)
то есть отнесенный к единице объема поток вектора F через поверхность бесконечно малого объема, окружающего рассматривающую точку.
Если в некоторой точке div F > 0, то эта точка является источником векторных линий; если div F < 0, то точка является стоком. При div F = 0 векторные линии непрерывны в точке, то есть не начинаются и не кончаются в рассматриваемой точке.
В декартовой системе координат
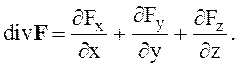(1.27)
Векторные поля, у которых div F = 0, называются свободными от источников или соленоидальными, то есть трубчатыми.
Важнейшая теорема, связанная с понятием дивергенции, есть теорема Гаусса-Остроградского о преобразовании поверхностного интеграла в объемный. Поток вектора через замкнутую поверхность равен объемному интегралу от дивергенции вектора
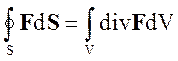(1.28)
Если вектор F соленоидальный, то поток этого вектора через любую поверхность S, натянутую на замкнутый контур L, не зависит от вида этой поверхности, а только от контура L. Введем понятие линейного интеграла вектора F вдоль кривой L. Для этого рассмотрим кривую L, соединяющую две точки М0 (r0) и М1 (r1), показанную на рис. 1.9.
Разобьем кривую на бесконечно малые элементы, которые заменим хордами dr, составим затем скалярные произведения F dr, где F есть вектор поля, отвечающий началу вектора dr. Составим далее сумму всех таких скалярных произведений и перейдем к пределу, устраняя все элементы dr к нулю.
Полученный предел называется линейным интегралом вектора F вдоль кривой L и обозначается через
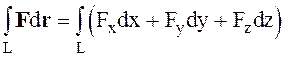(1.29)
Линейный интеграл вектора по замкнутой кривой называется циркуляцией вектора по этой кривой.
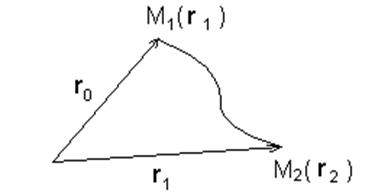
Рис.1.9. Понятие линейного интеграла.
Если j(х, у, z) - скалярное поле, то grad j = F порождает потенциальное векторное поле F. В этом случае линейный интеграл вектора F вдоль какой-либо кривой L, соединяющей точки M0 (r0) и M1 (r1) равен разности значений функции j в точках М1 и М0.
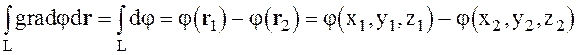(1.30)
В частности интеграл по замкнутой кривой будет равен нулю.
Обратное утверждение: если линейный интеграл вектора F вдоль всякой замкнутой кривой равен нулю, вектор F есть градиент некоторого скаляра j.
Согласно (1.30) линейный интеграл не зависит от пути, а определяется положением начальной и конечной точек М1 и М0.
Рассмотрим поле любого вектора F(r) (не обязательно потенциальное). Выделим плоскую площадку S, ограниченную контуром С. Такая площадка может быть представлена вектором
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.