Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 11

dA = F dl = q (E + [v, B]) dl = q E dl                      (2.57)

так как векторы V и dl совпадают по направлению, следовательно [V, B] dl = =[dl, V] B = 0. Мощность, определяемая как работа в единицу времени

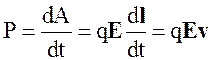 , [Вт]                                             (2.58)

Для объема DV заряд равен q = r DV, а мощность

DR = r DV E v                                                                   (2.59)

отсюда получаем

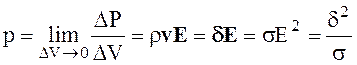                     (2.60)

При наличии сторонних источников

d = d_пр + d^ст  или  d = s(E + E^ст),                                    (2.61)

где d_ст - удельная плотность токов проводимости.

Закон Джоуля-Ленца с учетом сторонних источников принимает вид

p = dE = d_прE + d^стE = sE² + dE^ст                                             (2.62)

Согласно закону Джоуля-Ленца в дифференциальном виде мощность электромагнитного поля в точке в любой момент времени переходит в мощность потерь и мощность сторонних источников.

При рассмотрении некоторого объема V получаем закон Джоуля-Ленца в интегральном виде

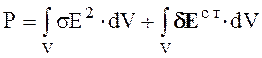                                                                                     (2.63)

или      R = R_n + R^ст                                                                                                                                     (2.64)

В случае R^ст > 0 энергия электромагнитного поля, заключенная в объеме V, тратится на потери и на переход в другие виды энергии.

При отрицательном значении R^ст < 0 возможны два варианта: если, , то на потери тратится как энергия сторонних источников, так и энергия электромагнитного поля; если,  то энергия сторонних источников тратится в объеме на потери и на увеличение энергии электромагнитного поля.

Мгновенный баланс энергии электромагнитного поля

Вывод уравнения баланса энергии производится с помощью умножения второго уравнения электромагнитного поля скалярно на вектор Н, а первого на вектор Е. Затем вычитают из результата первого умножения результат второго умножения

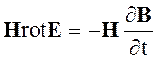
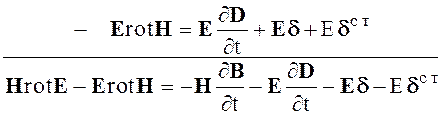
Используя тождество

div [E, H] = H rot E - E rot H

получаем

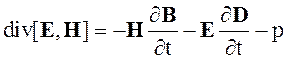,                                                              (2.65)

где p соответствует (2.61)

Для объема V, ограниченного замкнутой поверхностью S

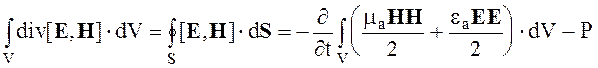                           (2.66)

Здесь использована формула Остроградского-Гаусса, значение D выражено как D = e_aЕ, значение В = m_aН.

Последний член выражения (2.66) согласно закону Джоуля-Ленца представляет собой мощность электромагнитного поля, расходуемую на потери и переход в другие виды. Член

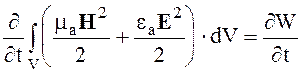                                                            (2.67)

представляет изменение запасенной в объеме V энергии магнитного и электрического полей.

Энергия магнитного поля в объеме V

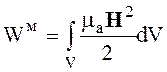,                                                                             (2.68)

энергия электрического поля

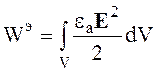                                                                                 (2.69)

Векторное произведение [E, H] называется вектором Пойтинга и обозначается как П. Вектор Пойтинга для любой незамкнутой поверхности есть плотность потока энергии, проходящей через единицу поверхности по направлению нормали к ней в рассматриваемой точке за одну секунду

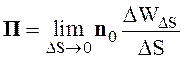,                                                                         (2.70)

где n₀ - нормаль к поверхности, DS - площадка, перпендикулярная n₀, DW_DS - количество энергии, проходящее через DS в одну секунду.

Интеграл

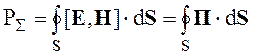                                                                        (2.71)

выражает поток энергии электромагнитного поля через замкнутую поверхность S, ограничивающую объем V в одну секунду. Здесь R_S называется мощностью излучения. Уравнение (2.66) теперь можно переписать в виде

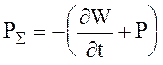                                                                               (2.72)

При значении R_S ¹ 0 происходит обмен энергией между полем в объеме и полем в окружающем объем пространстве. Возможны варианты обмена энергией между объемом V и внешним пространством

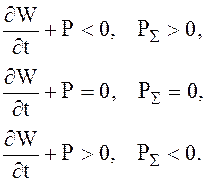                                                                    (2.73)