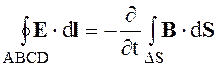Основы теории электромагнитного поля. Направленные электромагнитные волны и направляющие системы, страница 10

                                                      (2.43)

В пределах участков АD и ВС можно считать Е₁ и Е₂ постоянными, в пределах DS = DlDh - значение В постоянным. Следовательно,

,                 (2.44)

где С_бок =  .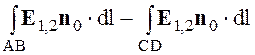

При Dh ® 0 (C_бок ® 0, DS ® 0) получим граничные условия для тангенциальных составляющих вектора Е

(E₁ - E₂)t₀ = [E₁ - E₂, n₀] = 0                                            (2.45)

Тангенциальные составляющие вектора Е всегда непрерывны при переходе через границу раздела. Умножая обе части уравнения (2.45) на e_a1 e_a2, получим граничные условия для тангенциальных составляющих вектора D

(e_a2D₁ - e_a1D₂)t₀ = [e_a2D₁ - e_a1D₂, n₀] = 0                          (2.46)

Граничные условия для векторов В и Н получают подобным же образом, используя оставшиеся два уравнения для векторов электромагнитного поля.

Нормальные составляющие вектора В всегда непрерывны при переходе через границу раздела

(B₁ - B₂) n₀ = 0                                                       (2.47)

Записывая В₁ и В₂ в виде B₁ = m_a1H₁ ; B₂ = m_a2H₂ , получаем граничные условия для нормальных составляющих вектора Н

(m_a1H₁ - m_a2H₂) n₀ = 0

Тангенциальные составляющие Н и В при наличии поверхностных токов

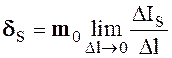                                                   (2.48)

удовлетворяют условиям

[H₁ - H₂ , n₀ ] = d_S                                                   (2.49)

[m_a2B₁ - m_a1B₂ , n₀ ] = m_a1 m_a2 d_S                                         (2.50)

В случае отсутствия поверхностных токов тангенциальные составляющие вектора Н непрерывна при переходе через границу раздела

(H₁ - H₂)t₀ = [H₁ - H₂ , n₀ ] = 0                                         (2.51)

Для тангенциальных составляющих в этом случае выполняются условия

(m_a2B₁ - m_a1B₂)t₀ = [m_a2B₁ - m_a1B₂ , n₀ ] = 0                                 (2.52)

Граничные условия на поверхности идеального проводника

Идеальный проводник обладает бесконечно большой проводимостью . Известно, что в идеально проводящую среду электромагнитное поле не проникает, поэтому все составляющие поля в среде 2 будут равны нулю. Граничные условия принимают вид

D₁ n₀ = r_S ;                       H₁ n₀ = 0 ,

E₁ n₀ =  ;                  B₁ n₀ = 0 ,                                 (2.53)

[E₁ , n₀] = 0 ;                   [H₁ , n₀] = d_S  ,

[D₁ , n₀] = 0 ;                   [B₁ , n₀] = m_a1 d_S .

На границе идеального проводника касательные составляющие векторов D и Е и нормальные составляющие векторов В и Н всегда равны нулю. Отсюда можно сделать вывод: векторные линии электрических составляющих электромагнитного поля всегда нормальны к поверхностям идеального проводника, а линии магнитных составляющих поля всегда касательны к ней.

2.4. Основные энергетические соотношения в теории электромагнитного поля.

Энергетические соотношения характеризуют движение, запас и преобразование энергии электромагнитного поля в другие виды энергии.

Закон сохранения энергии рассматривается в виде уравнений баланса энергии. В теории электромагнитного поля рассматривают два вида баланса энергии: баланс для мгновенных значений и баланс для средних значений.

При рассмотрении энергетических соотношений вводят понятие удельной объемной плотности мощности p и удельной запасенной энергии w

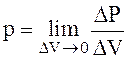 ,                                                         (2.54)

где  DR - мощность в малом объеме DV, переходящая в другие виды мощности, например, в мощность потерь.

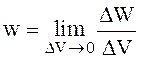,                                                        (2.55)

где DW - энергия, запасенная в малом объеме DV.

Закон Джоуля-Ленца

Закон Джоуля-Ленца устанавливает зависимость между мощностью электромагнитного поля, мощностью потерь и мощностью сторонних источников.

Закон Джоуля-Ленца можно получить из рассмотрения работы по перемещению электрического заряда в электромагнитном поле.

На заряд, движущийся в электромагнитном поле, со скоростью v действует сила F

F = q (E + [v, B])                                                    (2.56)

На пути dl в электромагнитном поле сила F совершает работу