Лекция 2.
Напряжения и токи на входе многополюсников.
Соотношения между напряжениями и токами на входах многополюсника полностью определяют матрицу сопротивлений (проводимостей) многополюсника.
Введем понятия нормированных значений напряжений и токов, как
величины ![]() и
и ![]() пропорциональные
суммарному поперечному электрическому полю
пропорциональные
суммарному поперечному электрическому полю 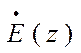 и
суммарному магнитному полю
и
суммарному магнитному полю 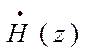 , соответственно.
, соответственно.
Падающей волне 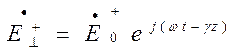 соответствует падающая
волна напряжения
соответствует падающая
волна напряжения 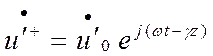 . Аналогично
. Аналогично
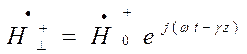 соответствует
соответствует 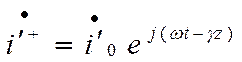 .
.
Из выражений, полученных в первой лекции, можно записать
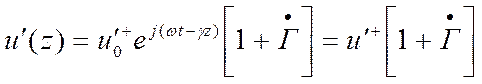 ,
,

Тогда комплексная мощность в сечении Z на входе
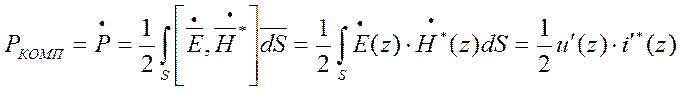 Сопротивление на входе полностью
определяется значениями
Сопротивление на входе полностью
определяется значениями ![]() и
и ![]() .
.
Их отношение полагается равным нормированному сопротивлению в сечении Z.
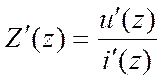
Теперь можно записать
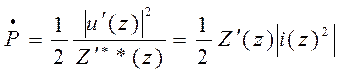
Можно получить коэффициенты пропорциональности между 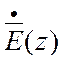 и
и ![]() и
и 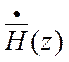 и
и ![]()
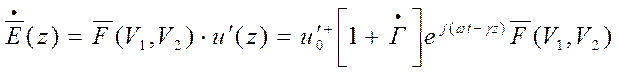 ,
,
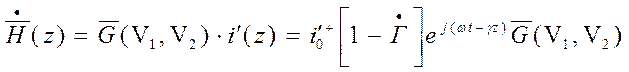 , где
, где 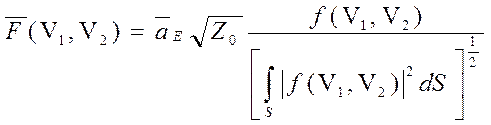 ,
,
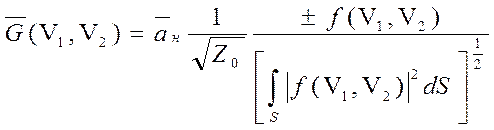 ,
,
V1, V2 – поперечные координаты в произвольной системе координат,
![]() - единичный вектор, совпадающий
по направлению с суммарной поперечной составляющей вектора
- единичный вектор, совпадающий
по направлению с суммарной поперечной составляющей вектора ![]() ,
,
![]() - единичный вектор, совпадающий
по направлению с суммарной поперечной составляющей вектора
- единичный вектор, совпадающий
по направлению с суммарной поперечной составляющей вектора ![]() .
.
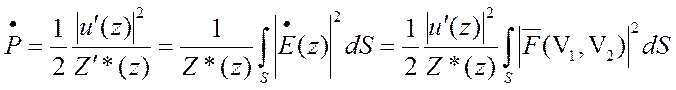
Из последенего выражения видно, что
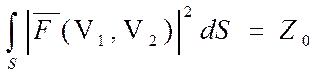
Аналогично можно показать, что
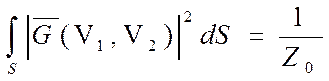
Выражения для конкретных типов волн в рассматриваемой линии
передачи можно получить из приведенных выше общих выражений для ![]() ,
, ![]()
1. Прямоугольный волновод, волна типа Н10
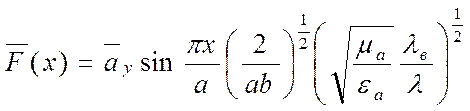 ,
,
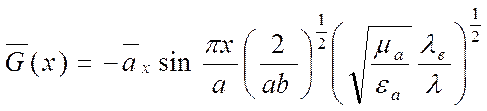 .
.
2. Круглый волновод, волна типа Н11
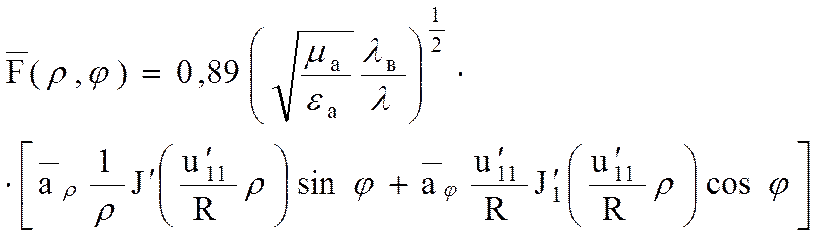
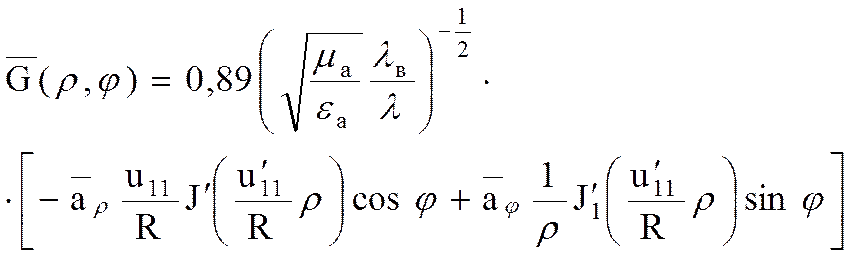 где
где ![]() -
корень уравнения
-
корень уравнения 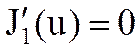 ,
,
R – радиус круглого волновода.
3. Коаксиальная линия, волна типа ТЕМ
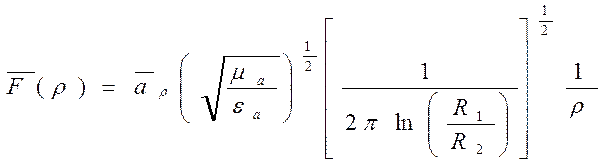 ,
,
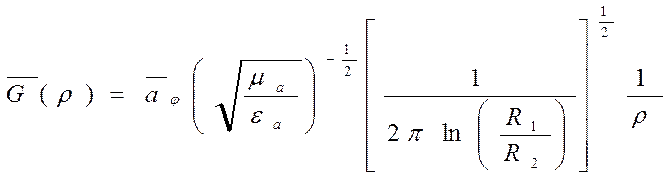 , где
R1, R2 – радиус внутреннего проводника и внутренний радиус
внешнего проводника, соответственно.
, где
R1, R2 – радиус внутреннего проводника и внутренний радиус
внешнего проводника, соответственно.
Все свойства цепей с распределенными параметрами могут быть перенесены на СВЧ соединения.
Рассмотрим 2n – полюсник, показанный на рисунке. Если среда, заполняющая 2n – полюсник, линейная и изотропная, то и уравнения Максвелла линейные, то есть выполняется принцип суперпозиции, и напряжение на входе р можно рассматривать как сумму «вкладов» соответствующих токов на входах 1, 2, …, р…, n и можно записать
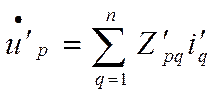
Полное входное сопротивление в сечении волновода, подключенного к плечу р определяется как
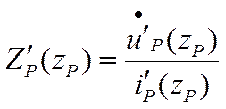
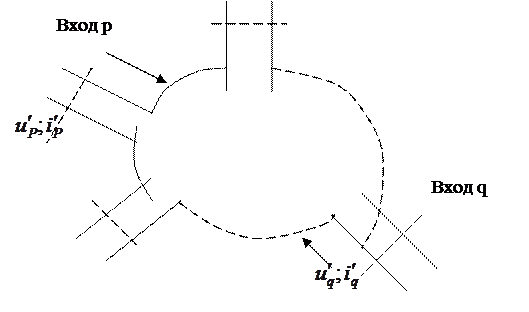 |
Рис. Схема 2n – полюсника.
Рассматривая напряжения на всех n входах по очереди получим совместную систему уравнений из n линейных уравнений
![]()
![]()
……………………………………
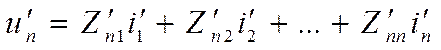
Эту систему можно записать в матричной форме
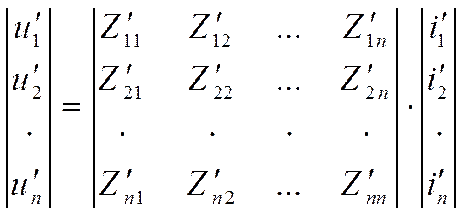
или
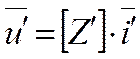 , где
, где
![]() и
и ![]() -
векторы столбцы,
-
векторы столбцы, ![]() - матрица сопротивлений.
- матрица сопротивлений.
Аналогично
можно получить и матрицу проводимостей ![]()
![]()
матрицы
столбцы (векторы) ![]() и
и ![]() являются
либо входными, либо выходными величинами. Матрицы
являются
либо входными, либо выходными величинами. Матрицы ![]() ,
, ![]() определяют те преобразования, которые
осуществляются многополюсником над векторами.
определяют те преобразования, которые
осуществляются многополюсником над векторами.
Основные теоремы теории цепей.
Теорема Пойтинга.
Рассмотрим уравнение баланса энергии для двухполюсника, показанного на рис. , в комплексном виде, считая, что стенки двухполюсника выполнены из идеальных проводников, однако внутри устройства имеют место потери.
 |
Рис. Двухполюсник с идеально проводящими стенками.
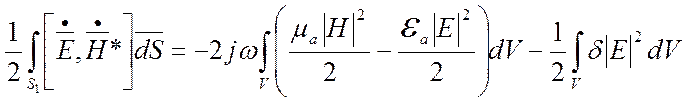 , то
есть комплексная мощность, выходящая через сечение S1 из рассматриваемого двухполосника
, то
есть комплексная мощность, выходящая через сечение S1 из рассматриваемого двухполосника
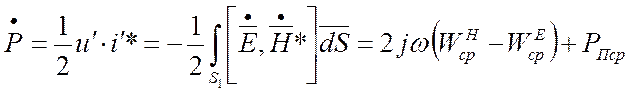
Здесь
направление вектора ![]() противоположно направлению тока
(см. рис. ).
противоположно направлению тока
(см. рис. ).
Значение
![]() , по этому можно записать
, по этому можно записать
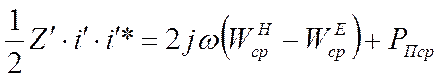 , откуда
, откуда
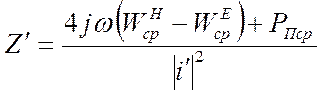
Аналогично можно получить
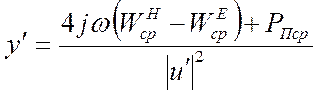
Легко обобщить полученный результат для 2n – полюсника
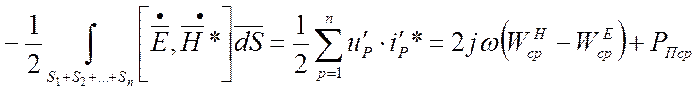
Лемма Лоренца.
Если
![]() и
и ![]() представляют
собой два различных решения уравнений Максвелла, удовлетворяющие граничным
условиям внутри рассматриваемого соединения (либо действуют на одной и той же
частоте два генератора СВЧ, либо рассматриваются два различных типа волн), то
имеет место равенство (при условии изотропной среды, заполняющей устройство)
представляют
собой два различных решения уравнений Максвелла, удовлетворяющие граничным
условиям внутри рассматриваемого соединения (либо действуют на одной и той же
частоте два генератора СВЧ, либо рассматриваются два различных типа волн), то
имеет место равенство (при условии изотропной среды, заполняющей устройство)
![]()
Интегрируя уравнение по объему устройства и применяя теорему Остроградского – Гаусса, получим
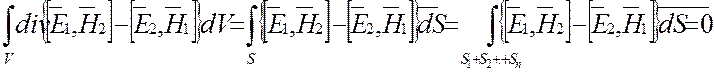
При двух решениях, соответствующих одному типу волны, т.е. если предполагается наличие двух генераторов СВЧ, так что
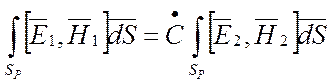 , где
, где
![]() - комплексный множитель, то с учетом
теоремы Пойтинга можно записать
- комплексный множитель, то с учетом
теоремы Пойтинга можно записать
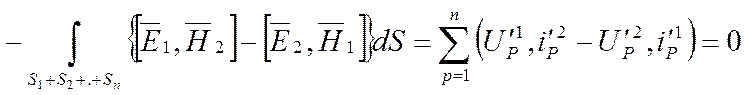
Свойство взаимности (обратности).
Является частным случаем Ленны Лоренца и заключается в том, что для линейного многополюсника, заполненного изотропной средой, выполняются соотношения
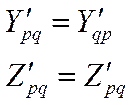
Теорема Фостера.
Теорема Фостера позволяет анализировать сложные многополюсники и синтезировать их из простых элементов подобно току, как гармонический анализ дает возможность анализировать и синтезировать периодические волны сложной формы путем разложения их на простые гармонические волны.
Можно показать [ ] приложение 2, что
![]() , где
в случае потерь
, где
в случае потерь 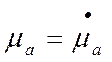 , а
, а 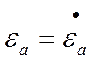 , а
, а
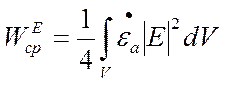 ;
; 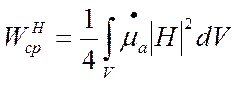
По определению
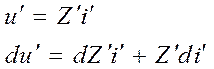
с учетом последнего выражения
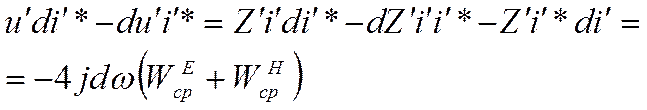
или
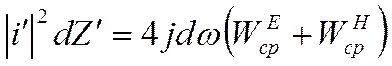 , так как
, так как ![]() .
.
Если
потери в двухполюснике отсутствуют, то ![]() является
чисто реактивным сопротивлением, то есть
является
чисто реактивным сопротивлением, то есть ![]() -
действительная величина.
-
действительная величина.
Запишем уравнение в виде
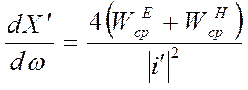
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.