В
случае отсутствия потерь все величины в правой части действительные и
положительные, поэтому 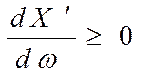 .
.
Следовательно, наклон кривой зависимости реактивного сопротивления от частоты всегда положительный.
Проводя аналогичные рассуждения и выводы можно получить
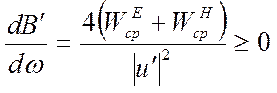 , то
есть кривая зависимости реактивной проводимости от частоты имеет всегда
положительный наклон.
, то
есть кривая зависимости реактивной проводимости от частоты имеет всегда
положительный наклон.
Обобщая полученные результаты для многополюсника, получим
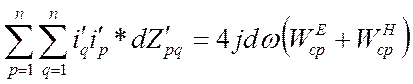 , или
, или
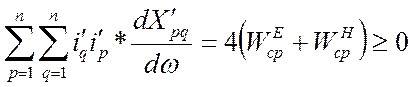 .
.
Последнее выражение можно привести к виду
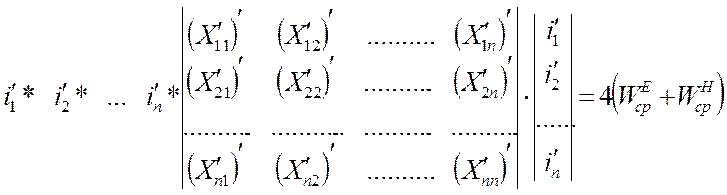 где
где 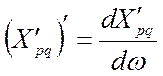 .
.
В
сокращенной форме 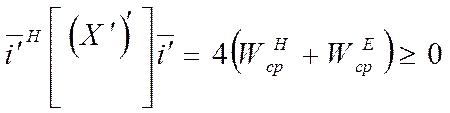
Отсюда
следует, что 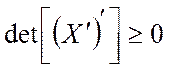
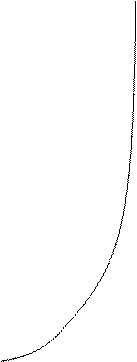
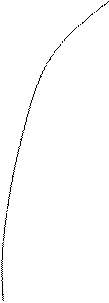
Зависимость изменения реактивного сопротивления от частоты имеет вид, показанный на рис.
 |
|||||||||||||||||||||
 |
 |
 |
|||||||||||||||||||
 |
|||||||||||||||||||||
 |
|||||||||||||||||||||
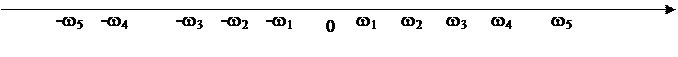 |
Рис. Зависимость реактивного сопротивления от частоты.
Из
выше полученных соотношений для 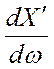 и
и ![]() можно сделать следующие выводы:
можно сделать следующие выводы:
1. Для устройств без потерь на частоте w = 0 реактивное сопротивление равно нулю, либо равно - ¥. При увеличении w, X` увеличивается, и если для конечных значений w X` стремиться к +¥, то при дальнейшем возрастании w X` переходит через значение - ¥. Между двумя полюсами кривая зависимости X` от частоты пересекает ось абсцисс: полюса и нули чередуются.
2. Функция X`(w) нечетная, так как наклон кривой X`(w) всегда положителен, даже при w = 0. Аналитически это записывается для любой частоты в виде
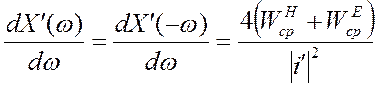
![]()
следовательно,
![]()
3. Из теории функций комплексных переменных известно, что две функции, имеющие одни и те же нули и полюсы в какой-либо области, равны с точностью до произвольной постоянной (имеют одинаковые разложения в ряд). Следовательно, на комплексной плоскости сопротивление X` полностью определяется своими полюсами и нулями с точностью до произвольной постоянной.
Выражение, определяющее значение X`, в общем виде как функция частоты, записывается так
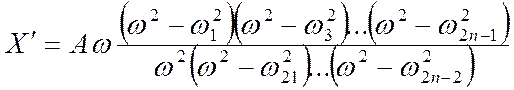 , где
w2, w4, …,wn-2 – положительные плюсы,
, где
w2, w4, …,wn-2 – положительные плюсы,
-w2, -w4, …, -wn-2 – отрицательные плюсы,
w1, w3, …,w2n-1 – положительные нули,
-w1, -w3, …,-w2n-1 – отрицательные нули,
А – постоянная.
На основании теории вычетов соотношение для X можно записать в виде
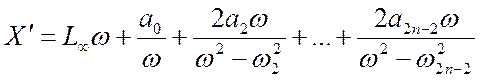 , где
L¥ =
A, а0, а2 … а2n-1 – называются вычетами в
полюсах 0, w2, …,w2n-2.
, где
L¥ =
A, а0, а2 … а2n-1 – называются вычетами в
полюсах 0, w2, …,w2n-2.
Значение
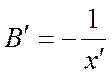 , поэтому имеем
, поэтому имеем
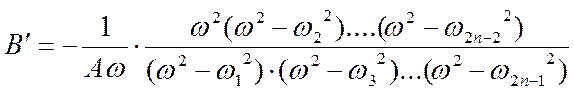 .
.
Или, используя значения вычетов
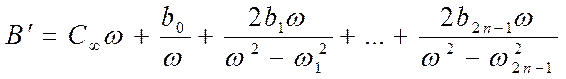 .
.
Из выражений видно, что полюсы для X` становятся нулями для B` , а нули для X` - полюсами для B`.
Если известна функция проводимости, то вычеты а0, а1 … а2n-2 могут быть вычислены.
В окрестности точки w2i
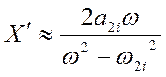 ,
, 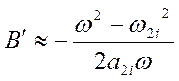
Наклон функции b`(w) в ее нуле w2i равен
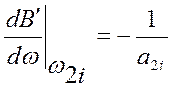 отсюда
отсюда 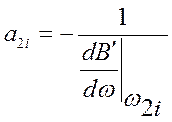
здесь i = 0, 1, 2…n-1
Первая эквивалентная схема.
Уравнение для X` соответствует ряду параллельных резонансных контуров, соединенных последовательно
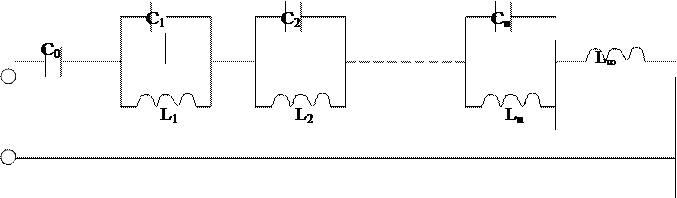
Рис. Первая эквивалентная схема (потери равны нулю).
Произвольное
слагаемое 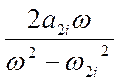 соответствует параллельному резонансному
контуру, причем
соответствует параллельному резонансному
контуру, причем 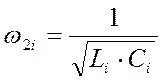 .
.
Полное сопротивление параллельного контура без потерь
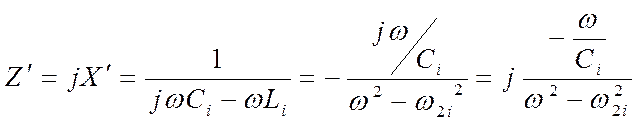
из сравнения формулы со схемой (рис. ) видно, что
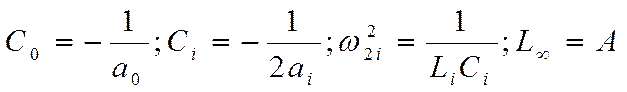
Вторая эквивалентная схема.
Составлена на основании формулы для проводимости B`
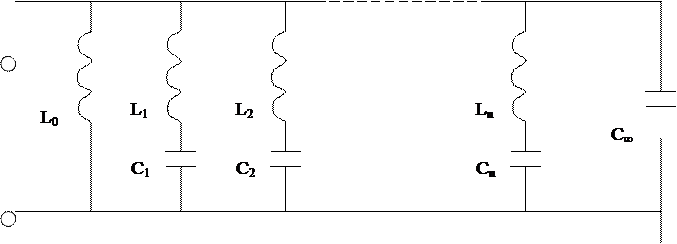
Рис. Вторая эквивалентная схема.
Произвольное
слагаемое 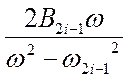 соответствует последовательному
резонансному Li Ci –
контуру, причем
соответствует последовательному
резонансному Li Ci –
контуру, причем
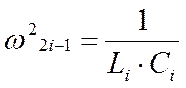 .
.
Полная проводимость последовательного резонансного контура без потерь составляет
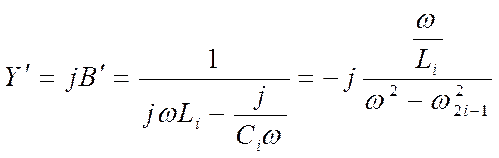
Из сравнения схемы с уравнением для b` видно, что
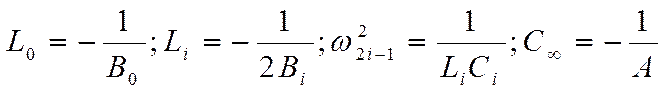
В большинстве практических случаев рабочий диапазон частот находится вблизи какого-либо одного полюса, а другие полюса находятся достаточно далеко и не оказывают влияния на реактивное сопротивление в рабочем диапазоне частот.
Практически любое СВЧ устройство имеет потери. Можно при выводе учесть и их наличие. При этом вместо jw вводится комплексная частота wкомп .
Однако удобнее предположить, что потери не велики и что количество энергии, рассеиваемой за период СВЧ колебаний, мало по сравнению с запасенной энергией и не оказывает существенного влияния на реактивное сопротивление.
При рассмотрении конкретных задач в таких случаях вводится понятие добротности.
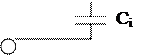
При этом типовой элемент эквивалентных схем состоит из трех элементов вместо двух, как показано на рис.
|
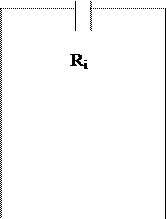 |
 |
||
![]()
![]()
![]()
|
 |
|||
|
|
Рис. Эквивалентная схема контуров с учетом небольших потерь.
а – параллельный контур,
b – последовательный контур.
Для схемы а) добротность ![]() ,
,
Для схемы b)
добротность 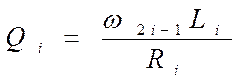
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.