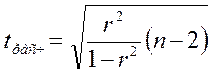Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 9

 или                                                                                                                   (2.11)

,                                                                                                                   (2.12)

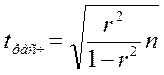
где n– число единиц в выборке

Примечание: формула 2.11 применяется при небольших выборках (не более 100 единиц), а формула 2.12 – при больших выборках (более 100 единиц)

Расчетное значение t_расч сравнивается с критическим значением (приложение 2) при n-2 степенях свободы и требуемом уровне значимости (0,05 или 0,01). Если расчетное значение оказывается больше критического, то делается вывод о том, что коэффициент корреляции значимо отличается от 0 и связь между анализируемыми признаками статистически значима.

Если коэффициент корреляции статистически значим, можно осуществить его интервальную оценку с использованием z-распределения Фишера. Расчетное значение z-статистики определяется по формуле:

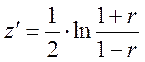                                                                               (2.13)

Доверительный интервал для  определится следующим образом:

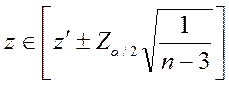                                                                 (2.14)

где Z_α/2 – значения нормального распределения для уровня значимости α.

Для того, чтобы определить доверительный интервал для самого коэффициента корреляции, необходимо выполнить обратное преобразование полученных границ:

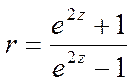                                                                                (2.15)

где вместо z требуется подставить границы доверительного интервала для , а r покажет значение соответствующей границы для коэффициента корреляции.

В том случае, если оценивается корреляция явления, зависящего более чем от одной независимой переменной, то необходимо определиться с тем, какую связь мы хотим оценить. Если оценивается связь между двумя переменными: результативной и одной объясняющей, то используют коэффициент частной корреляции.

В том случае, если всего используется три переменные, то коэффициент частной корреляции xи yпри условии постоянства zрассчитывается по формуле:

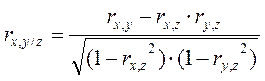                                                          (2.16)

Если же необходимо установить связь между всеми переменными, то рассчитывается коэффициент полной корреляции:

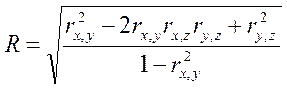                                                       (2.17)

Для решения конкретных задач в эконометрике используются также и другие показатели связи: коэффициент автокорреляции, коэффициент детерминации и др. Они будут рассмотрены в последующих темах.

Вопросы для самоконтроля

1)  Какие основные характеристики случайной величины Вы знаете?

2)  В чем сущность и различия точечных и интервальных оценок случайной величины?

3)  Охарактеризуйте основные свойства точечной оценки.

4)  В чем состоит противоречие между свойствами несмещенности и эффективности оценки?

5)  Опишите ковариацию как показатель связи. В чем ее основной недостаток?

6)  От каких факторов зависит величина ковариации?

7)  В чем отличие теоретической и выборочной ковариации?

8)  Для каких целей может применяется коэффициент корреляции?

9)  В каких приделах изменяется коэффициент корреляции?

10)  Для чего используют коэффициент частной корреляции?

11)  В чем особенность применения коэффициента общей корреляции?

Задания и задачи

1. Какие из приведенных оценок являются:
а) несмещенными;       б) эффективными:

2. При помощи трех различных методов проведена оценка средних расходов на питание в вузе. Определите, какая оценка является:

а) несмещенной         б) эффективной          в) состоятельной,

если истинное значение величины расходов составляет 14 рублей