Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 15

Рассмотренные модели также можно комбинировать, получая линейные преобразования для других исходных моделей.

Таблица 3.2

Линеаризация основных видов регрессионных моделей

В чем суть подхода Бокса-Кокса к подбору линеаризующего преобразования?

В оценке качества парных регрессионных моделей можно выделить следующие основные этапы (рис. 3.4):

1.  Анализ адекватности модели в целом

2.  Анализ точности определения оценок коэффициентов регрессии

3.  Проверка статистической значимости коэффициентов регрессионного уравнения

4.  Интервальная оценка коэффициентов регрессионного уравнения при заданном уровне значимости

5.  Определение доверительных интервалов для зависимой переменной (для среднего значения и для индивидуальных значений)

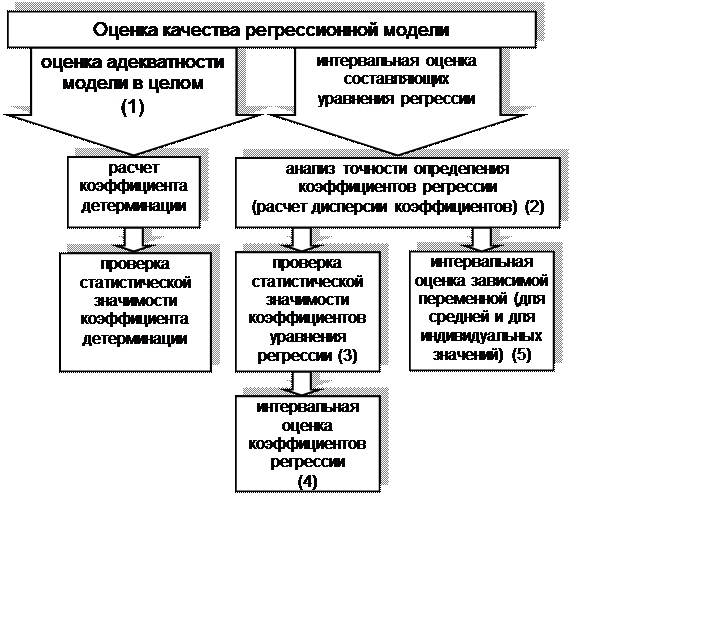
Рис. 3.4 Анализ качества регрессионной модели

Рассмотрим каждый этап подробно:

I. Для определения адекватности модели в целом используется теоретический коэффициент детерминации (коэффициент детерминации, R²).

Коэффициент детерминации показывает, какая доля вариации независимой переменной объяснена на основе построенной регрессионной модели:

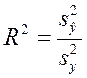                                                                                        (3.21)

где  – фактическая дисперсия зависимой переменной,  – дисперсия оценочных значений зависимой переменной, полученных на основании модели:

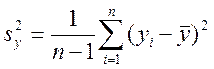                                                                   (3.22)

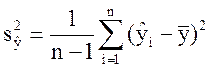                                                                   (3.23)

R² принимает значения от 0 до 1, причем чем ближе его значение к 1, тем лучше построенная модель описывает фактическую зависимость.

Так как , общая дисперсия  может быть представлена как сумма дисперсии объясненной составляющей  и дисперсии случайного остатка:

                                                                                (3.24)

где 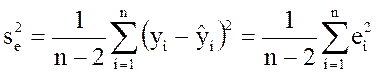                                 (3.25)

В этом случае формула (3.21) будет иметь вид:

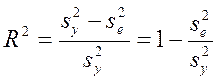,                                                                 (3.26)

откуда можно сделать вывод, что качество модели будет тем выше, чем меньше вариация случайного остатка.

После несложных преобразований получаем формулы, часто используемые в практических расчетах:

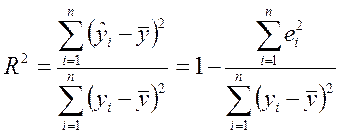                                              (3.27)

Значение теоретического коэффициента детерминации связано со значением линейного коэффициента корреляции между теоретическими и фактическими значениями результативного признака:

                                                                                         (3.28)

Вывод о приемлемости регрессионной модели для описания фактических данных можно сделать, учитывая объем анализируемой совокупности, число переменных и прочие факторы. Обычно значение R² не превышает 0,7 (исключение составляют временные ряды с четко выраженным трендом, для которых это значение приближается к 1). Для точной оценки статистической значимости коэффициента детерминации используют F-критерий:

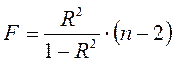                                                                          (3.29)

Полученное фактическое значение сравнивают с критическим F_α; 1; n-2, если расчетное значение оказывается больше критического, то нулевая гипотеза отвергается и делается вывод о статистической значимости коэффициента детерминации.