Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 33

5)  Возврат на шаг 2.

Основной проблемой применения этого метода является постоянное сокращение числа степеней свободы, из-за чего увеличиваются ошибки коэффициентов, а также часто возникающая проблема мультиколлинеарности.

2.  Метод геометрической прогрессии

В этой модели предполагается, что коэффициенты при лагах в зависимой переменной убывают в геометрической прогрессии:

, где λ – коэффициент, характеризующий скорость убывания коэффициентов с увеличением лага (0<λ<1)

В этом случае спецификация модели будет иметь вид:

                             (6.8)

то есть в модели будет 3 неизвестных параметра ().

Для расчета их значений используют два основных метода:

I.  Произведя замену  мы получаем линейную парную регрессию:

                                                                            (6.9)

Как видно, значения z_t зависят от неизвестного параметра λ, поэтому, прежде чем оценить параметры регрессии (6.9), следует определить, какое значение λ будет оптимальным. Однако строгого алгоритма для этого не существует, поэтому приходится действовать методом перебора: выбирают фиксированный шаг изменения λ (например, 0,01; 0,001; 0,0001) и для каждого λ от 0 до 1 рассчитывают значения z_t. Для полученной модели вида (6.9) можно провести оценку параметров , а также рассчитать коэффициент детерминации. Из построенных моделей выбирается та, которая обеспечивает наибольшее значение R².

Следует отметить, что количество лагов p задается таким образом, чтобы при увеличении их на единицу изменение z_t было бы меньше заранее выбранного малого числа Δ (например, если x_t описывает месячную заработную плату (в рублях), т.е. диапазоны ее изменения – от 500 до 10000, то Δ может быть порядка 1 – 10).

II.  Преобразование Койка. Этот метод достаточно широко распространен в эконометрическом анализе. Он реализуется следующим образом: из уравнения (6.6) вычитается такое же уравнение, только рассчитанное для периода (t-1) и умноженное на λ:

         (6.10)

Получаем уравнение:

                                     (6.11)

после несложных преобразований:

                                                    (6.12)

где  – скользящая средняя случайных остатков временного ряда – также случайная величина.

Преобразование модели вида (6.8) в модель вида (6.12) получила название преобразования Койка. Как видно из формулы, модель (6.12) является линейной регрессией с двумя объясняющими переменными и тремя неизвестными параметрами, оценить которые можно при помощи МНК.

Однако в этом случае возможны следующие проблемы, приводящие к несостоятельности и смещенности оценок, получаемых по МНК:

1.  Переменная y_t-1 носит случайный характер, и, кроме того, она, скорее всего, будет коррелировать с v_t, что приводит к нарушению предпосылок МНК.

2.  Для случайных отклонений v_t  вполне возможно наличие автокорреляции (см. ниже).

Для преодоления проблем, связанных с применением МНК, используют обобщенный метод наименьших квадратов (ОМНК). Основное отличие ОМНК в том, что для его применения необязательно выполнение предпосылок 2 и 3 МНК, касающихся взаимонезависимости случайных остатков и постоянства их дисперсии. Применение ОМНК требует знания дополнительной информации об остатках, получить которую чрезвычайно сложно, поэтому на практике часто используют частные случаи ОМНК – доступный метод наименьших квадратов [Кремер, Путко, стр. 185] и метод взвешенных наименьших квадратов.

Модель (6.12) можно применять для долгосрочного прогнозирования. Если предположить, что xстремится к своему равновесному значению x*, то:

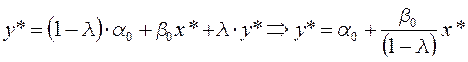                         (6.13)

Следовательно, мы можем определить равновесное значение зависимой переменной.

Вообще для временных рядов и динамических регрессионных моделей достаточно распространено явление автокорреляции (взаимозависимости) случайных остатков или просто автокорреляции.

К причинам возникновения автокорреляции относят: