Например, выборочная средняя является наилучшей оценкой генеральной средней, так как соответствует всем четырем свойствам.
Интервальная оценка представляет собой интервал, в котором с известной вероятностью находится истинное значение исследуемого признака. Такой интервал называется доверительным, а соответствующая ему вероятность – доверительной вероятностью. В практическом статистическом анализе большую ценность представляет именно интервальная оценка. Наряду с доверительной вероятностью (p) используют термин уровень значимости (α=1-p).
Рассмотрим общие принципы проведения интервальной оценки. Она проводится в виде определения доверительных интервалов – интервалов, в которых с известной вероятностью находится изучаемая переменная. Величина интервала прямо пропорциональна дисперсии рассматриваемой случайной величины и обратно зависима от требуемого уровня значимости. Обычно выбираются уровни значимости 0,1 (10%-й уровень значимости); 0,05 (5%-й уровень значимости); 0,01 (1%-й уровень значимости).
При построении доверительных интервалов для средней величины предполагается, в соответствии с центральной предельной теоремой, что выборочные средние распределяются по нормальному закону распределения с ожидаемым значением, равным генеральной средней. Исходя из этого, доверительные интервалы определяются на основе площади под кривой нормального распределения следующим образом:
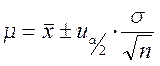, (2.6)
где uα/2 – значения, определяемые из таблицы площади под кривой нормального распределения; σ – генеральное среднеквадратическое отклонение; n – число единиц в выборке.
Интервальная оценка используется при анализе коэффициентов регрессии, значений зависимой переменной. Формулы для интервальной оценки представлены в соответствующих темах.
Выделяют следующие основные показатели связи:
1. Ковариация – абсолютный показатель связи двух показателей. Характеризует силу и направление линейной связи двух показателей. Различают теоретическую и выборочную ковариацию.
Теоретическая ковариация (
) – это математическое
ожидание произведения отклонений двух случайных величин от их средних значений.
Выборочная ковариация рассчитывается по формуле:
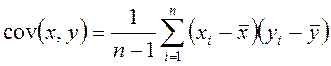(2.7)
Свойства ковариации:
1) cov(x,y) = cov(y,x)
2) cov(x,x) = sx2
3) если y = v + w, то cov(x,y) = cov(x,v) + cov(x,w)
4) если y = a*z, то cov(x,y) = a*cov(x,z)
5) если a = const, то cov(x,a) = 0
Существует альтернативная формула расчета ковариации:
(2.8)
Главным недостатком ковариации как показатели связи является то, что его значение зависит от единиц измерения исходных данных и не имеет критических значений, что затрудняет как сравнение различных совокупностей на предмет силы связи, так и делает невозможным установления критических значений ковариации.
Этот недостаток преодолевает следующий показатель связи – коэффициент корреляции. Он является относительным показателем связи и также характеризует силу и направление линейной связи двух признаков, изменяется в пределах от –1 до 1, чем ближе по модулю к единице, тем теснее связь между показателями.
Выделяют теоретический и выборочный коэффициент корреляции. Теоретический коэффициент корреляции рассчитывается по формуле:
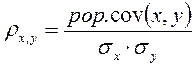(2.9)
где σx, σy – теоретическое среднеквадратическое отклонение xи yсоответственно.
Для расчета выборочного коэффициента корреляции используют формулу:
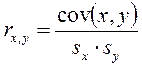, (2.10)
где sx и sy – выборочное среднеквадратическое отклонение x и y соответственно.
Вывод о наличии статистически значимой связи можно сделать, оценив значимость коэффициента корреляции. Это можно сделать при помощи t-критерия Стьюдента. Для этого проверяется гипотеза о равенстве этого коэффициента 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.