Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 36

№п/п

Значения DW

Вывод о наличии автокорреляции

1

[0;dlow)

существует положительная автокорреляция

2

[dlow;dhigh)

нельзя сделать вывод о наличии автокорреляции

3

[dhigh;4 – dhigh)

автокорреляция отсутствует

4

[4 – dhigh;4 – dlow)

нельзя сделать вывод о наличии автокорреляции

5

[4 – dlow;4]

существует отрицательная автокорреляция

Однако наряду с очевидными достоинствами критерия Дарбина-Уотсона существуют и ограничения его применения на практике:

1.  Критерий может применяться только для моделей, содержащих свободный член

2.  Временной ряд, по которому построена модель, должен быть полным (то есть внутри ряда должны быть все данные).

3.  Критерий Дарбина-Уотсона нельзя применять для авторегрессионных моделей AR(p).

4.  Критерий позволяет выявить автокорреляцию только первого порядка

Рассмотрим методы устранения автокорреляции. Выделяют два основных метода: при помощи первого устраняется сама автокорреляция, а при помощи второго возможно получение эффективных оценок коэффициентов и более точных значений их дисперсий. Рассмотрим каждый из методов:

1)  Изменение спецификации модели. Если автокорреляция является следствием неверной спецификации модели, то ее можно устранить путем изменения спецификации. Обычно в модель может быть добавлена периодическая составляющая (в виде тригонометрической функции – рис. 6.9) или учтен нелинейный характер изменений путем замены функции на логарифмическую или показательную в зависимости от характера отклонений (рис. 6.10).

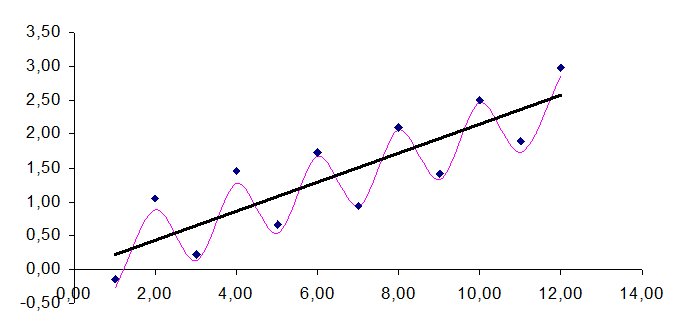
Рис. 6.9 Устранение отрицательной автокорреляции путем изменения спецификации модели с линейной функции на комбинированную (тригонометрическую-линейную)

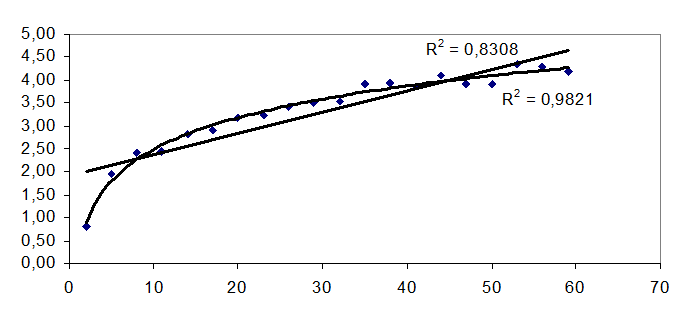
Рис. 6.10 Устранение автокорреляции изменением спецификации модели с линейной на логарифмическую

2)  Авторегрессионное преобразование. Для выполнения преобразования воспользуемся алгоритмом:

1.  Из исходной модели , в которой наблюдается автокорреляция, строим модель регрессионной зависимости между случайными остатками , которая будет удовлетворять предпосылкам МНК.

2.  Строим два уравнения для периодов t и t-1:

                                                                       (6.20)

                                                                 (6.21)

3.  Вычитаем из первого уравнения второе, умноженное на ρ:

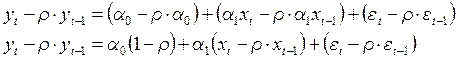
4.  Заменим: , тогда уравнение примет вид:

                                                                   (6.22)

К уравнению модели (6.22) можно применить МНК, так как для него случайные остатки удовлетворяют условиям Гаусса-Маркова. В результате применения МНК получаем оценки параметров a0* и a1.

5.  Зная параметр модели (6.17) a0*, определяем параметр исходной модели (6.20)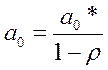

Авторегрессионное преобразование уменьшает число степеней свободы на 1, что при небольших объемах выборок приводит к снижению эффективности оценок. Это проблема решается при помощи поправки Прайса-Винстена:

                                                                                  (6.23)

                                                                                  (6.24)

Авторегрессионное преобразование применимо и в случае множественной регрессии.

Основная проблема, связанная с использованием авторегрессионного преобразования – оценка параметра ρ. Для этого используют следующие методы:

1. Статистика Дарбина-Уотсона. В этом случае предполагают, что при больших выборках . Тогда, используя соотношение , получим выражение для оценки ρ:

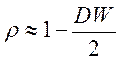                                                                                   (6.25)

2. Метод Кохрана-Оркатта. Этот метод относится к числу итеративных и основан на применении следующего алгоритма:

1) По МНК определяются параметры в регрессии:

                                                                                 (6.26)

Скачать файл