Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 53

Таблица 12

Интервальная оценка коэффициентов

коэф­фици­ент

значе­ние

ошибка коэффициента

интервальная оценка

s2

s

t-статистика

размер интервала

нижняя граница

верхняя граница

a0

57,26

4,90

24,04

11,68

9,61

47,65

66,88

a1

0,35

0,07

0,006

4,73

0,15

0,21

0,50

a2

3,911

3,01

9,054

1,30

5,90

-1,989

9,811

Сравнивая фактические значения t-статистики для коэффициентов (табл. 12) с критическими значениями (табл. 13), можно сделать вывод, что коэффициент перед a2 статистически незначим. С другой стороны, значения коэффициентов a0 и a1 практически не изменились, следовательно переменная является лишней, и ее не следует добавлять в модель.

Таблица 13

Критические значения t-статистики

№п/п

α (уровень значимости)

1.

0,1

2,31

2.

0,05

2,75

3.

0,01

3,83

Исключаем лишнюю переменную из модели, и в дальнейшем будем рассматривать парную линейную модель.

9. Проверим модель на наличие гетероскедастичности. Для этого используем метод графического анализа остатков и метод расчета рангового коэффициента Спирмена.

Поле корреляции между независимой переменной и квадратом случайной ошибки выглядит следующим образом (рис. 5)

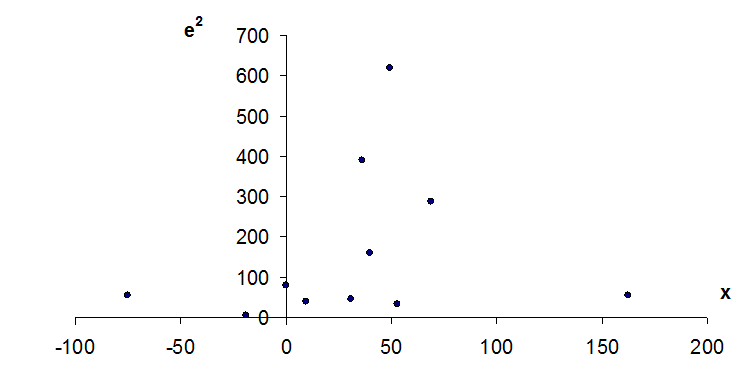
Рис. 5 Графический анализ остатков –
гетероскедастичность не обнаружена

По внешнему виду корреляционного поля нельзя сделать однозначный вывод о наличии (отсутствии автокорреляции). Необходимо проведение тестов. Рассчитаем ранговый коэффициент Спирмена. Для этого построим вспомогательную таблицу:

Таблица 14

Расчет коэффициента Спирмена

№п/п

X

e2

Ранг по x

Ранг по e2

d

d2

1

февр.

49,5

620,9

8

1

7

49

2

март

36,3

390,0

6

2

4

16

3

апр.

68,7

286,7

10

11

-1

1

4

май

-75,0

54,2

1

8

-7

49

5

июнь

53,0

33,0

9

5

4

16

6

июль

31,2

45,5

5

7

-2

4

7

авг.

0,1

81,9

3

10

-7

49

8

сен.

-18,9

5,6

2

4

-2

4

9

окт.

39,8

161,0

7

3

4

16

10

ноя.

9,6

40,5

4

6

-2

4

11

дек.

162,4

56,7

11

9

2

4

сумма

356,7

212

среднее

32,4

Ранговый коэффициент Спирмена равен:

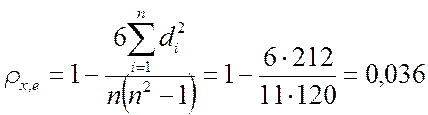
оценим статистическую значимость коэффициента Спирмена:

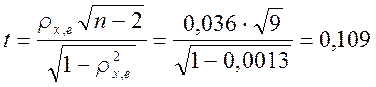
Критическое значение при пятипроцентном уровне значимости равно 2,69 (см. табл.6), что больше расчетного, следовательно, коэффициент Спирмена статистически незначим, и гетероскедастичность отсутствует.

! Самостоятельно убедитесь в отсутствии гетероскедастичности при помощи остальных тестов (Парка, Глейзера, Голдфельда-Квандта и Уайта)!

9.  Проверим модель на наличие автокорреляции.

9.1  Построим корреляционные поля (рис. 6 и 7). По их визуальному анализу нельзя сделать однозначный вывод о наличии или отсутствии автокорреляции.

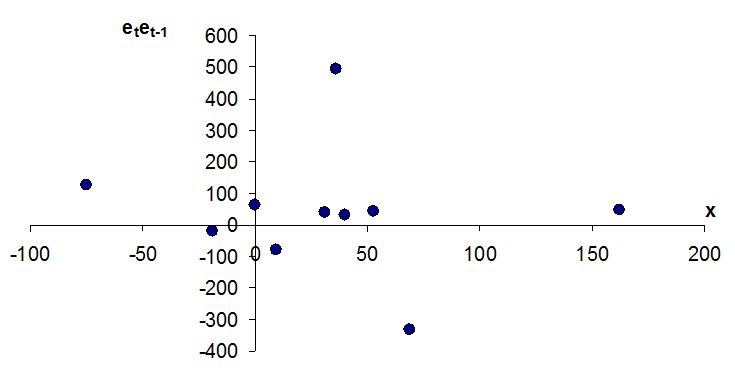
Рис. 6. Анализ автокорреляции

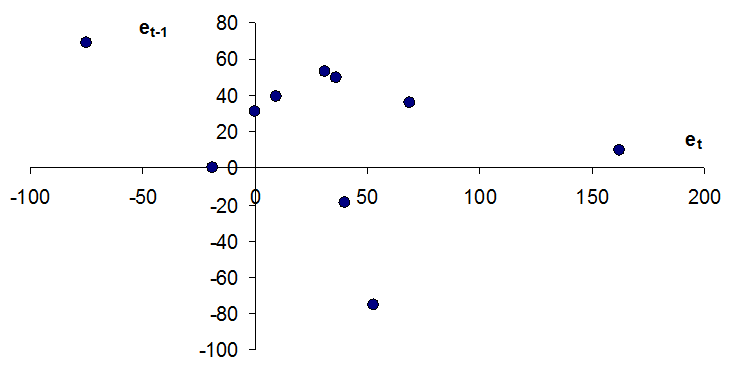
Рис. 7. Анализ автокорреляции (продолжение)

Скачать файл