Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 52

Обозначим прирост ставки по кредиту через . Матрица корреляций в этом случае будет иметь вид:

Таблица 10

Матрица корреляций между
выбранными статистическими признаками

x1

y

x1

1

0,23

0,86

-0,08

1

0,10

y

0,86

0,41

1

Переменная коррелирует и с y , и с x1. Для того, чтобы добавить переменную  в модель, необходимо убедиться в том, что нет мультиколлинеарности между объясняющими переменными. Для этого оценим качество регрессии . По методу наименьших квадратов получаем (проверьте!):

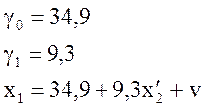
При этом качество модели характеризуется R2=0,053. Рассчитываем по формуле (4.10) F-критерий:

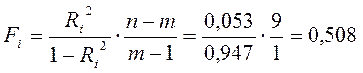
Критическое значение F-критерия при 5% уровне значимости меньше фактического (F0,05;1;9=5,117), следовательно, делаем вывод об отсутствии мультиколлинеарности.

Добавляем в модель переменную . Общий вид модели:

y=α0+α1x1+α2+ε

7. Для получения оценок по методу наименьших квадратов выполняем предварительные расчеты (какие расчеты необходимы?), составляем и решаем систему:

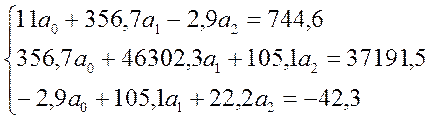
Результат ее решения:

a0=57,3

a1=0,353

a2=3,9

модель будет иметь вид:

y=57,3+0,353 x1+3,9+ e

8. Оценим качество построенной модели.

8.1 Расчет коэффициента детерминации. Построим вспомогательную таблицу:

Таблица 11

Оценка качества множественной модели линейной регрессии

№п/п

x1

y

e

e2

1

февр.

49,5

49,2

-2,0

66,93

-17,74

314,87

2

март

36,3

49,4

-0,1

69,70

-20,30

412,20

3

апр.

68,7

98,2

2,5

91,31

6,94

48,10

4

май

-75,0

34,7

-0,6

28,43

6,27

39,34

5

июнь

53,0

81,2

-2,5

66,21

14,95

223,64

6

июль

31,2

74,0

0,8

71,41

2,56

6,56

7

авг.

0,1

64,6

-1,1

53,00

11,59

134,42

8

сен.

-18,9

46,0

-1,5

44,72

1,31

1,72

9

окт.

39,8

57,8

0,3

72,50

-14,73

216,86

10

ноя.

9,6

65,5

1,0

64,57

0,91

0,83

11

дек.

162,4

124,0

0,3

115,80

8,24

67,86

сумма

356,7

744,6

-2,9

744,6

1466,4

среднее

32,4

67,7

-0,3

67,7

133,3

На основе таблицы рассчитываем коэффициент детерминации R2 = 0,780 (см. формулу 3.22)

Скорректированный коэффициент детерминации  равен 0,725 (см. формулу (4.6))

Проверим статистическую значимость коэффициента детерминации:

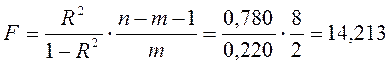
F0,01;2;8= 8,65 < Fрасч, коэффициент детерминации значим на однопроцентном уровне.

Определим, насколько существенно улучшилась модель (см. формулу 4.10)

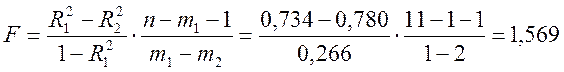
Расчетное значение оказывается меньше теоретического при пятипроцентном уровне значимости: F0,05;1;9= 5,117, что говорит о том, что модель существенно не улучшилась, и переменная является лишней или вредной.

8.2 Расчет дисперсий оценок коэффициентов и определение их статистической значимости, расчет доверительных интервалов. Для выполнения расчета ошибок коэффициентов необходимо использовать формулы, выделенные для самостоятельно изучения (см. тему 4). Расчет статистической значимости коэффициентов и доверительных интервалов выполнен по аналогии в парной регрессией (см. тему 3). Результат расчета представлен в таблице:

Скачать файл