
Рис. 7.1 Причины, последствия, методы обнаружения и
устранения
последствий гетероскедастичности
Рассмотрим методы обнаружения гетероскедастичности:
1. Графический анализ остатков. По результатам построения модели и расчета случайных остатков строят график на осях (xi;ei2) (рис. 7.2).
К достоинствам метода следует отнести простоту реализации и возможность выявления гетероскедастичности любой формы. В то же время при помощи этого метода нельзя количественно оценить наличие гетероскедастичности, вследствие чего возникают проблемы при практической реализации метода, к примеру, для наборов данных, представленных на рис. 7.3

Рис. 7.2 Графический анализ остатков. Определение наличия гетероскедастичности: a – дисперсия остатков возрастает; b – дисперсия остатков сначала убывает, потом возрастает

Рис. 7.3 Невозможность установления гетероскедастичности при помощи графического анализа остатков
2. Тест ранговой корреляции Спирмена. В этом случае рассчитывают коэффициент ранговой корреляции Спирмена между независимой переменной и случайными остатками:
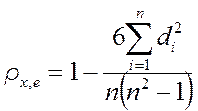 (7.1)
(7.1)
где di – ранговая разность между рангами значений xi и e2i.
Если связь оказывается статистически значимой, то делается вывод о наличии гетероскедастичности. Проверка статистической значимости связи осуществляется на основе t-статистики:
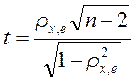 (7.2)
(7.2)
Полученное значение сравнивают с табличным значением tα/2,n-2. Если расчетное значение оказывается больше, связь между независимой переменной и случайными остатками признается статистически значимой, и делается вывод о наличии гетероскедастичности.
В случае множественной регрессии тест ранговой корреляции проводится отдельно для каждой переменной.
К достоинствам метода следует отнести простоту реализации и возможность сделать точный вывод о наличии (или отсутствии) гетероскедастичности. Основной недостаток метода – его неприменимость в случаях, когда дисперсии остатков изменяются не монотонно (как на рис. 7.2 (б)).
3. Тест Парка. Этот тест дополняет метод графического анализа остатков и основан на построении регрессионной зависимости дисперсии остатков от значения зависимой переменной:
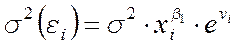 (7.3)
(7.3)
Модель (7.3) легко линеаризуется, и при помощи MHK можно получить оценку коэффициента β1. Затем оценивается статистическая значимость этого коэффициента. Если коэффициент статистически значим, то наличие гетероскедастичности считается доказанным. В случае анализа множественной регрессии тест проводится отдельно для каждой переменной.
Формально тест Парка можно представить в виде следующего алгоритма (рис. 7.4).
Достоинства теста Парка – существование жесткого критерия, позволяющего судить о наличии гетрероскедастичности. Недостаток – возможность необоснованных выводов, поскольку в тесте используется конкретная монотонно возрастающая (убывающая) функция. К примеру, применение теста к ситуации, изображенной на рисунке 7.1 (б), покажет, что гетероскедастичности нет.
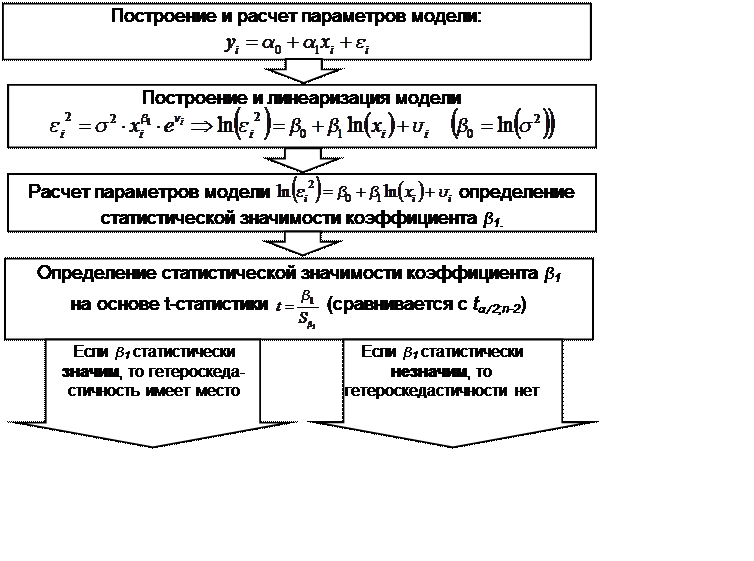
Рис. 7.4 Алгоритм применения теста Парка
4. Тест Глейзера по алгоритму применения аналогичен тесту Парка, однако за счет использования более универсальной функциональной зависимости он позволяет преодолеть недостаток теста Парка. В этом тесте используется функция:
![]() (7.4)
(7.4)
где k может принимать любые значения.
Обычно используются следующие значения k: –1; –0,5; 0,5; 1; 2. Модель (7.4) строится для каждого значения k, оцениваются ее параметры и проверяется статистическая значимость β1 . Если хотя бы в одном случае этот коэффициент оказывается статистически значимым, то гетероскедастичность имеет место.
Тест Глейзера позволяет установить наличие
гетероскедастичности даже в случаях немонотонного изменения функции ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.