Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 26

a)  m*m

b)  m*n

c)  (m + n) * (m + n)

d)  (m + 1) * (m + 1)

10.  Сумма диагональных элементов матрицы корреляции равна:

a)  m+1

b)  n

c)  2m

d)  m + n

11.  Какая из представленных формул предназначена для расчета ?

a) 

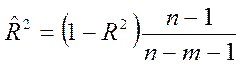
b) 

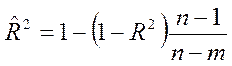
c) 

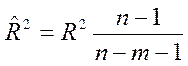
d) 

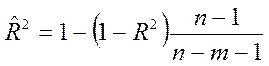
12.  Если мультиколлинеарность отсутствует, то определитель матрицы, составленной из коэффициентов корреляции независимых переменных, равен:

a)  0

b)  1

c)  числу независимых переменных

13.  На основе какого статистического критерия оценивается существенность добавления в модель переменной на основе сравнения коэффициентов детерминации?

a)  t-критерий Стьюдента

b)  F-критерий Фишера

c)  критерий хи-квадрат

14.  Какое значение коэффициента детерминации свидетельствует о том, что модель с 7-ю объясняющими переменными, основанная на анализе 30 единиц, статистически значима на 5%- уровне (F_0,05;6;20 = 2,60)?

a)  0,4 и больше

b)  0,5 и больше

c)  0,6 и больше

d)  0,7 и больше

Список литературы

1.  Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.ЮНИТИ, 1998. – с. 515 – 590; 621 – 672.

2.  Бородич С.А. Эконометрика: Учебное пособие. – Мн.: Новое знание, 2001. – с. 154 – 191; 271 – 280

3.  Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – XIV, с. 134 – 200

4.  Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – с.  82 – 100; 108 – 115; 124 – 130; 243 - 256

5.  Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2001. с. 83 – 89

6.  Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. 2-е изд. – М.: Дело, 1998. – с. 43 – 69; 74 – 90

7.  Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с. 49 – 105

8.  Теория статистики: Учебник / под редакцией Р.А. Шмойловой. – 3-е изд. – М.: Финансы и статистика, 1999. – с. 289 – 295

9.  Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с.90 – 175

Тема 5. Регрессионные модели с переменной структурой

5.1  Сущность и особенности использования фиктивных переменных

5.2  Модели ANOVA и ANCOVA

5.3  Вычисление параметров регрессионной модели с переменной структурой при помощи МНК

5.4  Оценка качества регрессионной модели с переменной структурой

5.5  Модели с фиктивной зависимой переменной

Основные положения

Часто возникает необходимость учета в регрессионной модели факторов, не имеющих количественного выражения. Например, при анализе динамики производства по месяцам следует учитывать сезонную компоненту. При анализе потребительских предпочтений может возникнуть задача учета пола потребителя, его отношения к определенной социальной группе. При регрессионном анализе предприятий может возникнуть потребность учета его формы собственности, отрасли, к которой предприятие относится. Модели, в которых учитываются подобные атрибутивные признаки, называются моделями с переменной структурой.

Для решения проблемы учета таких факторов можно:

1. Составить несколько регрессионных моделей, каждая из которых отражает зависимость в качественно однородной среде. Это приведет к значительному усложнению как непосредственно расчетов, так и интерпретации результатов.

2. Добавить в модель фиктивные переменные. Эти переменные могут принимать только два значения: 1, если наблюдается определенное значение признака, и 0, если оно не наблюдается. При этом количество переменных для включения одного признака будет на 1 меньше числа значений, принимаемых этим признаком.

Пример:

Рассмотрим регрессионную модель влияния на рентабельность активов различных факторов. Если необходимо учесть влияние фактора «организационно-правовая форма», то следует добавить следующие фиктивные переменные: