Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 50

№п/п	x₁	y					e²
№п/п	x₁	y	МС	МП	МВТ	МНК	МС	МП	МВТ	МНК
1	49,5	49,2	103,3	69,3	75,5	74,1	2931,4	405,3	690,6	620,9
2	36,3	49,4	75,8	68,1	69,8	69,1	695,8	348,3	415,7	390,0
3	68,7	98,2	143,4	71,1	83,7	81,3	2039,3	734,5	210,9	286,7
4	-75,0	34,7	-156,6	57,5	21,9	27,3	36577,2	518,0	164,0	54,2
5	53,0	81,2	110,6	69,6	77,0	75,4	868,4	132,6	17,6	33,0
6	31,2	74,0	65,1	67,6	67,6	67,2	78,3	41,0	40,8	45,5
7	0,1	64,6	0,2	64,6	54,2	55,5	4145,2	0,0	107,8	81,9
8	-18,9	46,0	-39,5	62,8	46,0	48,4	7307,4	281,2	0,0	5,6
9	39,8	57,8	83,1	68,4	71,3	70,5	640,5	112,8	182,7	161,0
10	9,6	65,5	20,0	65,5	58,3	59,1	2064,6	0,0	51,6	40,5
11	162,4	124,0	339,0	80,1	124,0	116,5	46203,6	1933,8	0,0	56,7
сум.	356,7	744,6	744,6	744,6	749,3	744,6	103551,6	4507,5	1881,7	1776,1
ср.	32,4	67,7	67,7	67,7	68,1	67,7	9413,8	409,8	171,1	161,5

Примечание:

МС – метод средних

МП – метод проб

МВТ – метод выбранных точек

МНК – метод наименьших квадратов

На основе таблицы для каждой модели по формуле (3.25) рассчитаем значение дисперсий случайного остатка, а по формуле (3.26) – значения коэффициента детерминации. Результат запишем в таблицу:

Таблица 5

Оценка адекватности моделей парной регрессии

№_п/п	Метод расчета	Дисперсия случайного остатка (s²_e)	Коэффициент детерминации (R²)
1.	Метод средних	10355,2	-14,509
2.	Метод проб	450,8	0,325
3.	Метод выбранных точек	188,2	0,718
4.	Метод наименьших квадратов	177,6	0,734

Как видно из таблицы, наилучшее качество имеет модель, построенная по методу наименьших квадратов.

Следующие этапы оценки качества проведем только для этой модели.

Для нее расчетное значение F-критерия равно:

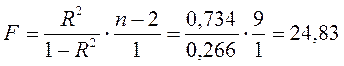
, а соответствующее критическое значение (приложение 3) – F_0,05;1;9= 5,117. Поскольку расчетное значение больше критического, то модель признается статистически значимой.

4.2. Вычислим дисперсии оценок коэффициентов регрессии. Для этого воспользуемся формулами (3.30) и (3.31):

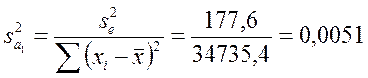
Стандартные ошибки коэффициентов регрессии будут равны:

4.3. Оценим статистическую значимость коэффициентов регрессии. Для этого рассчитаем t-статистику для каждого коэффициента (см. формулу 3.27):

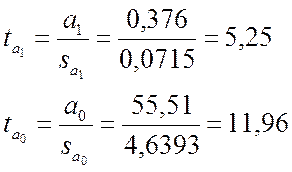
Сравним с критическими значениями, взятыми из таблицы (приложение 2):

Таблица 6

Критические значения t-статистики

№_п/п	α (уровень значимости)
1.	0,1	2,26
2.	0,05	2,69
3.	0,01	3,69

Можно сделать вывод, что коэффициенты регрессии статистически значимы при 1 %-м уровне значимости.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

Скачать файл