Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 20

                                                          (4.1)

Обычно рассматривают линейную модель, поскольку, как было показано в предыдущей теме, большинство нелинейных моделей достаточно легко сводятся к линейной путем линеаризации. Спецификация модели линейной множественной регрессии имеет вид:

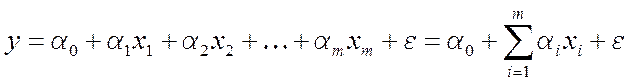        (4.2)

Уравнение линейной множественной регрессии будет выглядеть следующим образом:

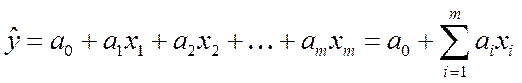                (4.3)

В случае применения множественного регрессионного анализа особое внимание следует уделить вопросам отбора переменных для анализа. Для этого используются два подхода: «сверху вниз» и «снизу вверх». Достоинства и недостатки каждого подхода были рассмотрены в теме 1, поэтому мы сразу затронем вопрос практической их реализации. На первом этапе построения модели составляется матрица корреляции размером (m+1) x (m+1), где m – общее число всех возможных независимых переменных (факторов). В нее помещаются коэффициенты корреляции между факторами и результативным признаком, а также попарно между всеми факторами. В ячейке r_ij указывается коэффициент корреляции между i-м и j-м фактором. Эта матрица будет симметричной относительно главной диагонали, причем на диагонали будут значения, равные 1:

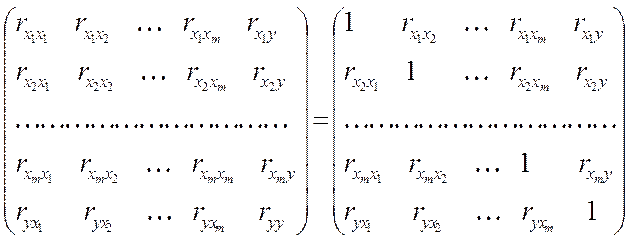        (4.4)

После этого в модель включаются факторы, для которых значение r_ij по модулю больше заданного критического значения. Обычно критическое значение устанавливают на уровнях 0.5 – 0.9. В то же время не следует включать в модель переменные, между которыми наблюдается тесная взаимосвязь (высокие значения r_ij в соответствующей ячейке). невыполнение этого условия может привести к некорректному построению модели (см. мультиколлинеарность).

По аналогии с парной регрессией для определения параметров множественной регрессии могут использоваться различные методы, однако чаще всего применяется МНК. Для его применения необходимо выполнение следующих предпосылок:

1.  Математическое ожидание случайного отклонения равно 0 для всех наблюдений M(ε)=0

2.  Дисперсия случайных отклонений постоянна

3.  Случайные отклонения независимы друг от друга

4.  Случайное отклонение независимо от объясняющих переменных регрессионной модели:

5.  Модель линейна относительно параметров

6.  Отсутствие сильной взаимозависимости между объясняющими переменными

7.  Случайные ошибки имеют нормальное распределение

При выполнении перечисленных предпосылок неизвестные коэффициенты уравнения регрессии a₁, a₂,… a_m найдутся из решения системы уравнений:

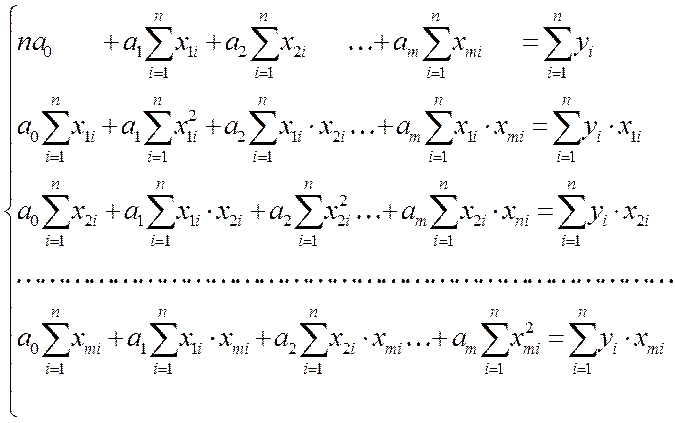   (4.5)

где количество уравнений совпадает с числом переменных (m+1), а суммирование осуществляется по выборке из n единиц.

Эта система может быть решена либо каким-нибудь из вычислительных методов линейной алгебры (например, методом Жордана-Гаусса), либо при помощи компьютера (в частности, такая функция реализуется в MS Excel).

Для множественной регрессионной модели актуален вопрос о том, какова сила влияния различных факторов на значение зависимой переменной. Для этого используются два основных метода. Первый основан на построении регрессионной модели в стандартизированной форме, второй – на расчете частных коэффициентов эластичности.

Для преобразования модели к стандартизованной форме осуществляют переход к новым переменным:

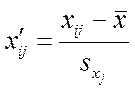                                                                                   (4.6)

уравнение множественной регрессии примет вид:

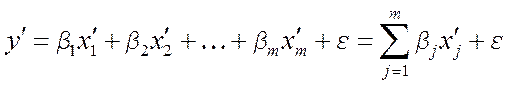                    (4.7)

Оценив параметры этой модели по МНК, по значениям параметров β_j при каждой переменной мы можем сделать вывод о сравнительной силе влияния различенных факторов. Большее значение коэффициента говорит о большей силе влияния соответствующего фактора на зависимую переменную, положительное значение – о прямом влиянии, отрицательное – об обратном.

Частные коэффициенты эластичности рассчитываются по формулам:

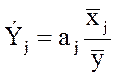                                                                                      (4.8)

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении зависимой на 1 процент и неизменности действия прочих факторов.