3.5. Линеаризация нелинейных моделей
3.6. Оценка качества парных регрессионных моделей
3.7. Ограничения использования регрессионных моделей
Парная регрессионная модель (регрессия) – это эконометрическая модель, описывающая зависимость между двумя факторами. Общий вид такой модели:
(3.1)
Наиболее простой и часто использующейся является линейная парная регрессионная модель, имеющая вид:
(3.2)
Выражение 3.2 представляет собой спецификацию линейной регрессионной модели. Вообще под спецификацией модели понимают аналитическое выражение описывающей модель функции.
Само уравнение линейной регрессии имеет вид:
(3.3)
где a0 и a1 – оценки теоретических коэффициентов регрессии α0 и α1
Следовательно, регрессионную модель можно представить
в виде: 
, где 
– объясненная
на основе построенной модели составляющая y, а ε – чисто
случайная составляющая.
Основная задача регрессионного анализа после спецификации модели – оценка неизвестных параметров – α0 и α1, дающих наибольшее приближение модели к эмпирическим данным:
(3.4)
где a0 и a1 – оценки неизвестных параметров; e – оценка случайной компоненты.
Для определения коэффициентов можно использовать различные методы (рис. 3.1):
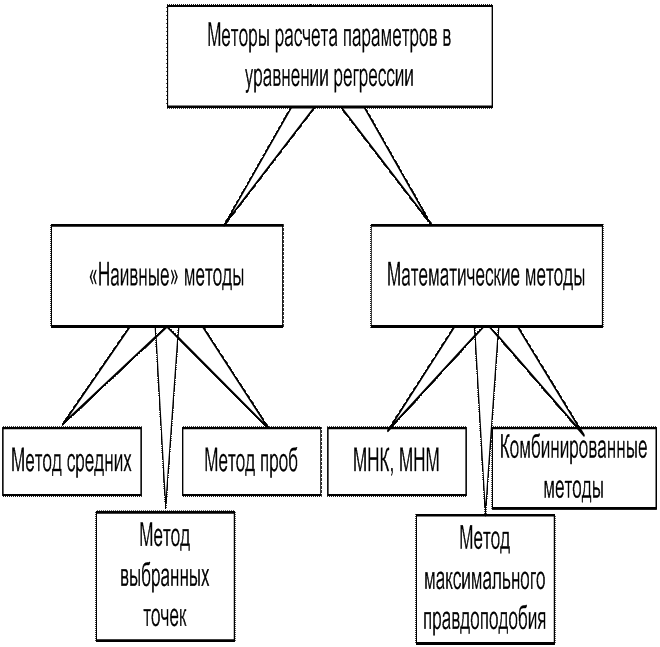
Рис. 3.1 Основные методы расчета коэффициентов регрессии
Метод средних применяется в том случае, когда в уравнении регрессии присутствует только один неизвестный параметр (например, a1 – y = a1x). В этом случае его значение определится следующим образом:
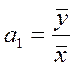(3.5)
Метод проб заключается в том, что всем параметрам, кроме одного, задаются фиксированные значения, исходя из особенностей эмпирических данных. Значение последнего, неизвестного параметра определяется по методу средних. Например, если зафиксировать значение, принимаемое yпри x, равном 0 (нулевой уровень y – y0), то параметр a1 определится по формуле:
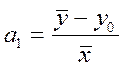(3.6)
Эта процедура может повторяться (для различных зафиксированных значений) до тех пор, пока качество теоретической модели не станет удовлетворительным.
Метод выбранных точек основан на визуальном анализе корреляционного поля и выборе точек, наиболее точно отражающих тенденции развития анализируемого явления. Количество точек должно совпадать с количеством неизвестных параметров. Так, для парной линейной регрессии выбирается 2 точки. Через них проходит только одна прямая, уравнение которой определится как решение системы относительно a0 и a1:
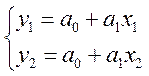, где (x1;y1) и (x2;y2) – координаты выбранных точек.
В результате решения такой системы можно рассчитать значения a0 и a1 по формулам:
Перечисленные методы
могут применяться для «быстрого», поверхностного анализа параметров уравнения
регрессии. Полученные на их основе оценки не обладают свойствами несмещенности,
эффективности, состоятельности и достаточности, поэтому для серьезного
исследования необходимо применять другие методы. Наибольшее распространение
получили такие математические методы, как метод наименьших модулей и метод
наименьших квадратов. Существуют также методы, совмещающие достоинства этих
методов, и преодолевающие их недостатки (в частности, функция Хубера).
В общем виде смысл математических методов можно определить как решение задачи минимизации функционала F, формируемого на основе суммирования отклонений эмпирических данных от результата расчета (чисто случайных составляющих) по регрессионной модели:
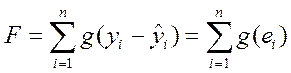, (3.9)
где g() – функция, определяющая аналитическую форму измерения разброса фактических данных от модели.
Наиболее распространены два вида функции g():
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.