Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 4

                                                       (1.5)

d.  модели тренда и сезонности (нестационарные циклические модели):

·  аддитивные:

                                              (1.6)

·  мультипликативные:

                                                (1.7)

e.  комбинированные динамические факторные модели

                                                  (1.8)

3)  модель системы одновременных уравнений

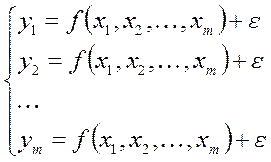                                                (1.9)

В зависимости от количества изучаемых факторов – объясняющих переменных – (xi, i=1..m) различают парную (m=1) и множественную (m>1) эконометрическую модель.

Затем выбирается функциональная форма эконометрической модели на основе анализа существующих статистических данных. Выбор формы модели зависит от характера эмпирической зависимости, устанавливаемой либо по корреляционному полю, либо с использованием специальных методов, изучаемых в теории статистики, либо на основании теоретических расчетов.

Для моделей, содержащих только одну объясняющую переменную, основные виды моделей выглядят следующим образом (табл. 1.1)

Таблица 1.1

Основные функциональные формы эконометрических моделей

№п/п

Вид модели

Аналитическое выражение

Соответствующее корреляционное поле

1.

Линейная

, где α0– начальный уровень y,
α 1– скорость изменения y при росте x

2.

Парабо­лическая

где α 0– начальный уровень y,
α 1– скорость изменения y при росте x,

α 2– величина ускорения изменения у при росте х

3.

Степен­ная

, где α0– начальный уровень y,
α1 и α2– параметры, характеризующие скорость изменения y при росте x

1. 0 < α2 < 1

2. α2 > 1

4.

Показа­тельная

, где (α0 + α1) – начальный уровень y,
α1 и α2– параметры, характеризующие скорость изменения y при росте x

1. 0 < α2 < 1

2. α2 > 1

5.

Логариф­мическая

, где α0– уровень y при x=1,
α1 и α2– параметры, характеризующие скорость изменения y при росте x

1. 0 < α2 < 1

2. α2 > 1

6.

Гипербо­лическая

, где α0– уровень y при x à∞,
α1 –скорость уменьшения y при росте x

α2 – предельное значение х, начиная с которого начинает убывать y

7.

Логисти­ческая

, где α0– предельное значение ряда ,
α1 – параметр, характеризующий начальное значение фактора x, α2 – скорость изменения y

1. α2 < 0; α0 > 0

1. α2 > 0; α0 > 0

8.

Тригоно­метри­ческая

, где α0– значение ряда, вокруг которого осуществляется колебательный процесс
α1 – амплитуда колебания y,
 α2 – скорость изменения y

9.

Комбинированные

Подпись: Продолжите таблицу для лог-линейных и линейно-логарифмических функций

Как видно из таблицы, для описания одних и тех же эмпирических данных вполне могут подойти различные формы моделей. В этом случае выбор полностью зависит от воли исследователя. При прочих равных условиях предпочтение отдается более простым моделям, содержащим наименьшее число параметров (в частности, линейной модели).

4. На следующем этапе происходит определение параметров эконометрической модели. Для этого существует целый ряд методов (метод выбранных точек, метод проб, метод наименьших модулей и т.п.), однако наибольшее распространение получили метод наименьших квадратов (МНК) и метод максимального правдоподобия (ММП).

5. Оценка качества модели. После определения параметров модели необходимо оценить, насколько хорошо она согласуется с эмпирическими данными, а также насколько существенно значение каждого параметра. При проверке адекватности всей модели используется коэффициент детерминации (R2), а для проверки значимости коэффициентов – метод статистической проверки гипотез относительно равенства каждого параметра 0 (или 1). Если гипотеза отвергается, то параметр признается значимым.

Скачать файл