Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 28

Общую характеристику качеству построенной модели может дать коэффициент детерминации  (поскольку модель множественной регрессии, то рекомендуется использовать скорректированный коэффициент детерминации , рассчитываемый по формуле (4.7)). Статистическая значимость коэффициента детерминации может быть оценена при помощи F-критерия.

В том случае, если использовалась мультипликативная форма модели (5.5) с одной фиктивной переменной, для оценки качества модели может быть использован тест Чоу.

Тест Чоу основан на F-критерии. Для его проведения необходимо построить регрессионную модель без участия фиктивной переменной (общую модель), рассчитать сумму квадратов отклонений фактических значений от общей модели. F-критерий рассчитывается как соотношение величины, на которую уменьшилась дисперсия в модели с переменной структурой по сравнению с общей моделью и дисперсии модели переменной структурой:

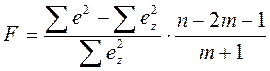                                                          (5.9)

где     – сумма квадратов случайных отклонений в общей модели

– сумма квадратов случайных отклонений в регрессионной модели с переменной структурой

Полученное фактическое значение сравнивается с критическим Fα; m+1; n-2m-1. Если расчетное значение оказывается больше фактического, то считается, что использование фиктивной переменной целесообразно.

Также фиктивная зависимая переменная может быть использована для интерпретации влияния на качественный признак количественных факторов. В этом случае говорят о фиктивной зависимой переменной.  Различают несколько видов таких моделей:

1.  Линейная вероятностная модель (linear probability model – LPM)

2.  Модели бинарного выбора (LOGITи PROBITмодели).

Спецификация линейной вероятностной модели имеет вид (4.2) – если все объясняющие переменные описывают количественные факторы, или (5.5) – если в модели присутствуют фиктивные объясняющие переменные. Однако в этом случае зависимая переменная y может принимать только одно из двух значений:

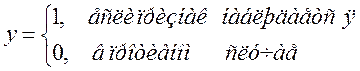                                           (5.10)

После расчета параметров модели по МНК расчетные значения зависимой переменной интерпретируются как вероятность того, что признак, характеризуемый y, будет наблюдаться. Однако применение этого метода ограничено тем, что:

1)  не выполняется ряд предпосылок МНК (случайные остатки не распределены по нормальному закону, дисперсия остатков непостоянна);

2)  возможна ситуация, когда расчетное значение y будет находиться вне области допустимых значений: [0,1];

3)  с содержательной точки зрения линейное изменение вероятности при изменении влияния факторов некорректно.

Для преодоления последних двух условий разработаны и используются модели бинарного выбора, среди которых выделяют LOGITи PROBITмодели.

Рассмотрим суть LOGITмодели. В ней в качестве функции, характеризующей вероятность того, что y примет значение 1, рассматривается логистическая функция. Эта функция принимает значения строго от 0 до 1:

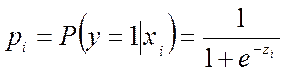                                                       (5.11)

где

Однако для применения МНК необходимо выполнить преобразования, поскольку функция (5.11) не линейна относительно параметров. Из (5.11) следует:

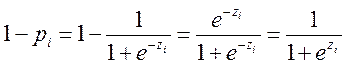                                             (5.12)

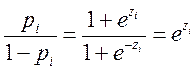                                                                      (5.13)

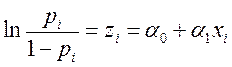                                                                (5.14)

Последнее выражение линейно относительно параметров, однако к нему нельзя применить МНК. Причина этого в том, что для фактических данных неизвестными остаются значения pi . Для их нахождения в случае сгруппированных данных возможно использование в качестве оценки относительную частость проявления 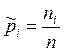, в случае несгруппированных следует применять метод максимального правдоподобия.

Вопросы для самоконтроля

1.  В каком случае возникает необходимость использования фиктивных переменных? Приведите примеры.

2.  Какие значения принимает фиктивная переменная? От чего зависит то, какое значение она примет?

Скачать файл