4. Использование предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров модели могут быть определены по пробным выборочным наблюдениям, тогда мультиколлинеарность может быть устранена путем установления значений параметра у одной коррелирующих переменных. Ограниченность метода – в сложности получения предварительных значений параметров с высокой точностью.
5. Преобразование переменных. Для устранения мультиколлинеарности можно преобразовать переменные, например, путем линеаризации или получения относительных показателей, а также перехода от номинальных к реальным показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки зрения обеспечения ее высокого качества возникают следующие вопросы:
1. Каковы признаки качественной модели?
2. Какие ошибки спецификации могут быть?
3. Каковы последствия ошибок спецификации?
4. Какие существуют методы обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели множественной регрессии:
1. Простота. Из двух моделей примерно одинаковых статистических свойств более качественной является та, которая содержит меньше переменных, или же более простая по аналитической форме.
2. Однозначность. Метод вычисления коэффициентов должен быть одинаков для любых наборов данных.
3. Максимальное соответствие. Этот признак говорит о том, что основным критерием качества модели является коэффициент детерминации, отражающий объясненную моделью вариацию зависимой переменной. Для практического использования выбирают модель, для которой расчетное значение F-критерия для коэффициента детерминации б четыре раза больше табличного.
4. Согласованность с теорией. Получаемые значения коэффициентов должны быть интерпретируемы с точки зрения экономических явлений и процессов. К примеру, если строится линейная регрессионная модель спроса на товар, то соответствующий коэффициент при цене товара должен быть отрицательным.
5. Хорошие прогнозные качества. Обязательным условием построения качественной модели является возможность ее использования для прогнозирования.
Одной из основных ошибок, допускаемых при построении регрессионной модели, является ошибка спецификации (рис. 4.3). Под ошибкой спецификации понимается неправильный выбор функциональной формы модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1. Невключение в модель полезной (значимой) переменной.
2. Добавление в модель лишней (незначимой) переменной
3. Выбор неправильной функциональной формы модели
Последствия ошибки первого вида (невключение в модель значимой переменной) заключаются в том, что полученные по МНК оценки параметров являются смещенными и несостоятельными, а значение коэффициента детерминации значительно снижаются.
При добавлении в модель лишней переменной (ошибка второго вида) ухудшаются статистические свойства оценок коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели и затрудняет содержательную интерпретацию параметров, однако по сравнению с другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор функциональной формы модели, то есть допущена ошибка третьего вида, то получаемые оценки будут смещенными, качество модели в целом и отдельных коэффициентов будет невысоким. Это может существенно сказаться на прогнозных качествах модели.
Ошибки спецификации первого вида можно обнаружить только по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней является только одна переменная, осуществляется на основе расчета t - статистики для коэффициентов. При лишней переменной коэффициент будет статистически незначим.
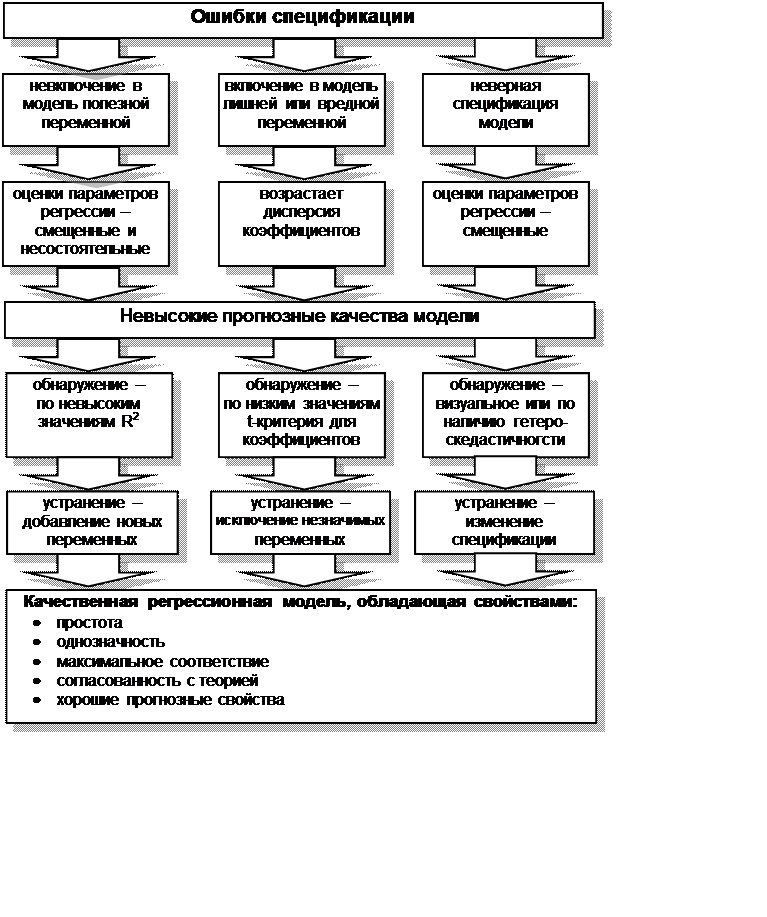
Рис. 4.3 Ошибки спецификации и свойства качественной регрессионной модели
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.